Natural Numbers

What Natural Numbers Are

The set of natural numbers consists of the numbers commonly used to count and order objects.

Natural numbers originated primarily as a means of counting collections of objects.

By convention, the set of natural numbers starting from 1 is denoted by N.

$$ N = \{ 1, 2, 3, 4, ... \} $$

Note. The concept of "zero" emerged much later than the other numbers. The earliest numbers used by humans were 1, 2, 3, and so on. Concepts such as one unit or two units have been familiar since prehistoric times because they are directly tied to concrete reality. Even some animals appear to possess this ability. For instance, crows seem capable of recognizing and counting three to four objects. Zero, by contrast, is an abstract concept that represents absence and was introduced much later in the historical development of mathematics.

The set of natural numbers that includes zero is denoted by N₀.

$$ N_0 = N \cup \{ 0 \} = \{ 0, 1, 2, 3, 4, ... \} $$

There is, however, no universally accepted convention.

Note. In some mathematics textbooks, the set N₀ is simply denoted by the symbol N, without any explicit distinction. In other contexts, the set N₀ is referred to as the set of non-negative integers.

Natural numbers are equipped with a well-defined order relation.

Given any two distinct natural numbers, it is always possible to determine whether one is less than or greater than the other.

Every natural number has a successor and, with the exception of the first element, a predecessor.

Example. The number 7 has successor 8 $$ 7+1 = 8 $$ and predecessor 6 $$ 7-1=6 $$

The only exception is the first element of the set of natural numbers, for example zero in N₀ or one in N, which has no predecessor.

Representation of Natural Numbers

Natural numbers can be represented on an oriented half-line.

We draw a half-line starting from an origin point O, which corresponds to the first natural number, zero or one depending on the chosen convention.

We fix a direction (arrow) and a unit of length (u).

We then mark the natural numbers, starting from the successor of 1 and continuing indefinitely.

Since every natural number has a successor, it follows that there are infinitely many natural numbers. Consequently, the set of natural numbers is an infinite set.

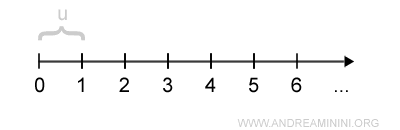
Each natural number corresponds to a point on the half-line. However, not every point on the half-line corresponds to a natural number.

Between any natural number and its successor, for example between 2 and 3, there exist infinitely many other points on the half-line.

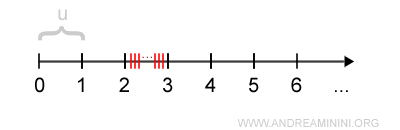
For this reason, the set of natural numbers is also described as a discrete set.

Operations on Natural Numbers

The natural numbers admit two closed operations.

• Addition
  The sum of two natural numbers is itself a natural number.

  Example. The sum of the natural numbers 5 and 7 is a natural number regardless of the order of the addends. $$ 5+7=7+5=12 \in N $$

• Multiplication
  The product of two natural numbers is itself a natural number.

  Example. The product of the natural numbers 5 and 7 is a natural number regardless of the order of the factors. $$ 5 \cdot 7=7 \cdot 5=35 \in N $$

The sum and the product of two natural numbers are again natural numbers. For this reason, addition and multiplication are called internal operations in N.

Note. Equivalently, one may say that the set of natural numbers is closed under addition and multiplication. The meaning is identical.

Inverse Operations

The inverse operations of addition and multiplication on natural numbers are subtraction and division, respectively.

• Subtraction
  The difference between two natural numbers a-b, where a is called the minuend and b the subtrahend, is defined as the number that, when added to the subtrahend b, yields the minuend a.

  Example. The difference of the natural numbers 7 and 5 is the natural number 2. $$ 7-5=2 \in N $$ because adding the difference (2) to the subtrahend (5) yields the minuend (7) $$ 2+5=7 $$

• Division
  The division of two natural numbers a:b, where a is the dividend and b the divisor, yields a number called the quotient q which, when multiplied by the divisor b, equals the dividend a.
  

  Example. The division of 8 by 2 yields the natural number 4. $$ 8:2=4 \in N $$ because the product of the quotient (4) and the divisor (2) equals the dividend (8) $$ 4 \cdot 2 = 8 $$

The set of natural numbers is not closed under subtraction and division.

Subtraction is not an internal operation in N because the result is not always a natural number.

Example. The difference of the natural numbers 5 and 7 is the number -2, which is not a natural number. $$ 5-7 = -2 $$ This is not an internal operation in N because there is no natural number n ∈ N such that $$ n+7=5 $$

In particular, within the natural numbers, subtraction is defined only when the minuend is greater than or equal to the subtrahend.

$$ \text{minuend } \ \ge \ \text{subtrahend} $$

Example. The difference between 7 and 5 is a natural number. $$ 7-5 = 2 \in N $$ The difference between 5 and 7, by contrast, is not a natural number $$ 5-7=-2 \notin N $$

To make subtraction an internal operation, it is necessary to introduce another numerical set, the set of integers (Z).

Division is not an internal operation in the set of natural numbers for two reasons.

• Division by zero is impossible because if a natural number n were divisible by 0, there would exist a natural number q such that q⋅0 = n. However, any number multiplied by zero is always equal to zero. Therefore, the operation is undefined.
  $$ \text{divisor} \ \ne \ 0 $$
• Dividing a natural number (the dividend) by another nonzero natural number (the divisor) does not necessarily yield a natural number.

Example. The division of the natural numbers $$ 5:2=q $$ does not yield a natural number because there is no natural number q in N such that $$ q \cdot 2=5 $$ In this case, the quotient of 5:2 is the real number 2.5 $$ 5:2=2.5 $$

Division between two natural numbers is possible only when the division is exact, that is, when the quotient is also a natural number.

Note. Alternatively, division between two natural numbers can be considered by introducing the concept of a remainder, known as non-exact division. $$ \text{dividend = divisor ⋅ quotient (q) + remainder (r)} $$ For example, dividing the natural numbers $$ 5:2=q+r $$ yields a quotient q=2 with remainder r=1. $$ 2 \cdot 2 + 1 = 5 $$

Axioms of the Natural Numbers

The set of natural numbers is described by the following axioms.

1. The set of natural numbers is closed under addition and multiplication
   
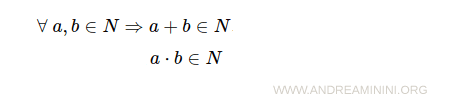
2. Commutative property of addition and multiplication
   
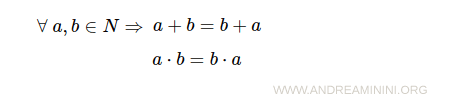
3. Associative property of addition and multiplication
   
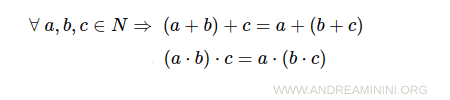
4. Distributive property of multiplication over addition
   
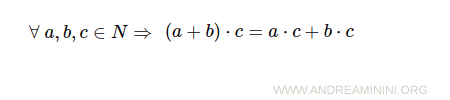
5. Existence of a multiplicative identity
   The multiplicative identity is the number 1. Multiplying any natural number a ∈ N by 1 leaves it unchanged.
   
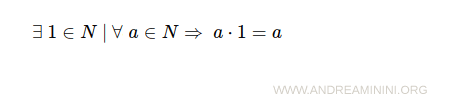
   The multiplicative identity is unique. See proof of the uniqueness of the identity element.

   Note. When considering the set of natural numbers N₀, which also includes zero $$ N_0 = N \cup \{ 0 \} = \{ 0, 1, 2, 3, 4, ... \} $$ it is also necessary to introduce the additive identity, sometimes referred to as the sixth axiom of the non-negative integers. For every n ∈ N, the sum n + 0 or 0 + n equals n $$ \forall n \in N \Rightarrow n + 0 = 0 + n = n $$ Moreover, within the natural numbers, a sum equals zero if and only if both addends are zero $$ 0 + 0 = 0 $$ Zero is also the absorbing element of multiplication, from which follows the zero-product property. The product of any natural number with zero is always zero, for example $$ 3 \cdot 0 = 0 \cdot 3 = 0 $$

Taken together, these five axioms characterize the algebraic structure of the natural numbers.

A more fundamental and widely used axiomatization of the natural numbers is given by the Peano axioms.

Successor Element

Given any number a in N₀, its successor is the element a + 1 $$ \forall a \in N_0 \rightarrow a + 1 \in N_0 $$

The notion of a successor follows directly from the sixth axiom of the non-negative integers N₀.

Since every natural number has a successor, it follows that the set of natural numbers is infinite.

Peano Axioms

The mathematician Giuseppe Peano introduced a rigorous axiomatization of the natural numbers through a collection of fundamental statements known as the Peano axioms.

1. There exists a natural number 0.
2. Every natural number has a successor $$ \sigma(n) = n + 1 $$
3. No natural number has zero as its successor $$ \sigma(n) \ne 0 $$
4. Distinct natural numbers have distinct successors $$ \sigma(a) \ne \sigma(b) $$
5. Every subset U of N that contains zero and is closed under the successor operation coincides with the entire set of natural numbers $$ \begin{cases} 0 \in U \\ \\ \forall k \in U \Rightarrow \sigma(k) \in U \end{cases} $$ This postulate is known as the principle of mathematical induction, sometimes informally described as the domino principle.

According to the Peano axioms, the natural numbers are specified by a set N, a successor function σ, and a distinguished element 0.

$$ \{ N, \sigma, 0 \} $$

The function σ is injective because it assigns to each natural number n a unique successor n + 1.

$$ \forall n \in N \rightarrow \sigma(n) = n + 1 $$

The element 0 does not belong to the image of the function σ because, by definition, it is not the successor of any natural number.

Note. As axioms, these statements are accepted without proof.

Minimum Principle

The minimum principle, also known as the well-ordering principle, is another fundamental property of the natural numbers.

Every non-empty subset M of the natural numbers N has a minimum element.

More precisely, given any non-empty subset T of N, there exists an element m in T such that m ≤ t for every t in T.

$$ \forall t \in T \:\: \exists \:\: m \in T \:\:|\:\: m \le t $$

Example

In the subset T₁ of N, the minimum element is zero.

$$ T_1 = \{ n \in N \:\:|\:\: n \le 5 \} $$

In the subset T₂ of N, the minimum element is the number 2.

$$ T_2 = \{ n \in N \:\:|\:\: n \ge 2 \} $$

Note. This property is specific to the natural numbers. In the set of integers or real numbers, there exist non-empty subsets that do not admit a minimum element. For example, the subset of integers less than or equal to 2 has no minimum element $$ T = \{ z \in Z \:\:|\:\: z \le 2 \} $$

The set of natural numbers N is said to be well-ordered because every non-empty subset has a minimum element.

And so on.