Uniqueness of the Multiplicative Identity

The multiplicative identity is unique and coincides with the number one (1).$$ \exists \ 1 \in N \ | \ \forall \ a \in N \Rightarrow a \cdot 1 = a $$

Multiplication by one leaves every natural number unchanged.

Example

$$ 5 \cdot 1 = 5 $$

Proof

The goal is to establish the uniqueness of the multiplicative identity in the natural numbers.

There are two logically incompatible possibilities.

1. The multiplicative identity is unique.
2. The multiplicative identity is not unique.

If the first statement holds, then the second must be false, and conversely.

Assume, for the sake of contradiction, that there exist two distinct multiplicative identities, 1 and ε.

$$ \exists \ 1 \in N \ | \ \forall \ a \in N \Rightarrow a \cdot 1 = a $$

$$ \exists \ \epsilon \in N \ | \ \forall \ a \in N \Rightarrow a \cdot \epsilon = a $$

Because both are assumed to be identity elements for multiplication, multiplying any natural number a by either 1 or ε yields the same result, namely a.

In particular, taking a = 1 and multiplying it by ε gives 1.

$$ a \cdot \epsilon = 1 \cdot \epsilon = 1 $$

Likewise, taking a = ε and multiplying it by 1 gives ε.

$$ a \cdot 1 = \epsilon \cdot 1 = \epsilon $$

Multiplication in the natural numbers satisfies the commutative property (second axiom of the natural numbers).

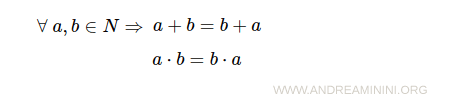
Setting a = 1 and b = ε, we therefore have

$$ 1 \cdot \epsilon = \epsilon \cdot 1 $$

Since 1·ε = 1 and ε·1 = ε, it follows that

$$ \underbrace{1 \cdot \epsilon} _1 = \underbrace{ \epsilon \cdot 1 }_{ \epsilon } $$

This equality shows that ε and 1 must denote the same natural number.

$$ 1 = \epsilon $$

Therefore, within the natural numbers, there exists no multiplicative identity other than the number one.

This completes the proof of the uniqueness of the multiplicative identity.

And so on.