Rational Numbers
What Rational Numbers Are
The set of rational numbers consists of all numbers that can be written as the ratio of two integers m and n, with n different from zero $$ Q = \{ \frac{m}{n} : m, n \in Z, n \ne 0 \} $$ This set is denoted by the symbol Q.
The set of rational numbers includes
- integers
- terminating decimal numbers
- repeating (periodic) decimal numbers
Note. Infinite non-repeating decimal numbers do not belong to the set of rational numbers because, lacking any repeating pattern, they cannot be expressed as the ratio of two integers. Such numbers are called irrational numbers, since they are not rational.
The set of rational numbers contains the set of natural numbers N and the set of integers Z as subsets.
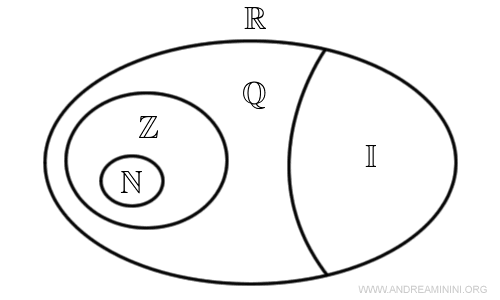
In turn, the set of rational numbers is itself a subset of the set of real numbers R.
All real numbers (R) that do not belong to the set of rational numbers (Q) are called irrational numbers (I).
A Practical Example
Example 1
The number 2.5 is a rational number because it can be expressed as the ratio of two integers, m = 5 and n = 2.
$$ 2.5 = \frac{5}{2} \in Q $$
Example 2
The number 5 is a natural number and an integer, but it is also a rational number because it can be written as the quotient of 15 and 3.
$$ 5 = \frac{15}{3} \in Q $$
Note. Any natural number or integer can be represented as the ratio of two integers. Consequently, the sets of natural numbers and integers are subsets of the set of rational numbers.
Example 3
Repeating decimal numbers are also rational numbers because they can be expressed as the ratio of two integers.
$$ 3.\bar{3} = \frac{10}{3} \in Q $$
Operations on Rational Numbers
Within the set of rational numbers, the following operations are defined
- Addition
$$ a+b = c \ \ \ \ a,b,c \in Q $$ - Subtraction
$$ a-b = c \ \ \ \ a,b,c \in Q $$ - Multiplication
$$ a \cdot b = c \ \ \ \ a,b,c \in Q $$ - Division
$$ a : b = c \ \ \ \ a,b \in Q \ c \in Q $$ - Exponentiation
$$ a^b = c \ \ \ \ a,b \in Q \ c \in Q $$
Note. Addition, subtraction, multiplication, and division are internal operations on the set of rational numbers Q, meaning that their results are always rational numbers.
Representation of Rational Numbers
To represent rational numbers, one draws a number line by fixing a direction, an origin point (O), and a unit of length.
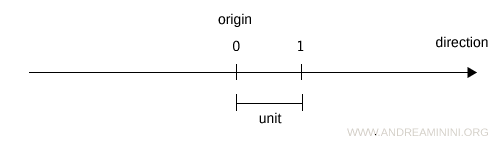
Once the line has been drawn, each rational number is associated with a corresponding point on the line.
For example, all fractions with denominator equal to 1 correspond to specific points on the line.
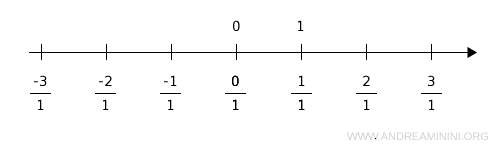
Fractions with denominator equal to 2 determine additional points on the line.
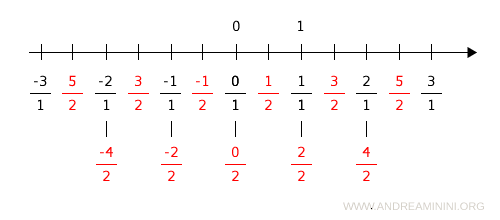
However, some of these points coincide.
For instance, the rational numbers 1/1 and 2/2 correspond to the same point on the number line.
The same is true for 0/1 and 0/2, or for 2/1 and 4/2, and so on.
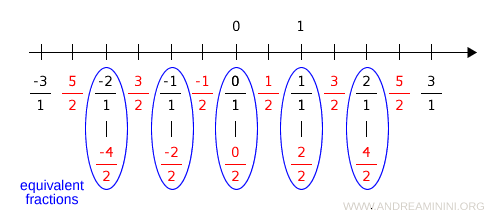
This happens because a rational number can be represented by infinitely many equivalent fractions, all of which identify the same point on the number line.
As rational numbers continue to be placed on the line, another fundamental property becomes apparent.
Between any two distinct rational numbers, there exist infinitely many rational numbers.
This property is expressed by saying that the set of rational numbers is a dense set.
For example, consider the rational numbers 1/2 and 1/4.

Between them, there is a midpoint.
$$ \frac{ \frac{1}{2} + \frac{1}{4} }{2} = \frac{ \frac{2+1}{4} }{2} = \frac{ \frac{3}{4} }{2} = \frac{3}{4} \cdot \frac{1}{2} = \frac{3}{8} $$
The rational number 3/8 is an intermediate point located exactly halfway between 1/2 and 1/4.
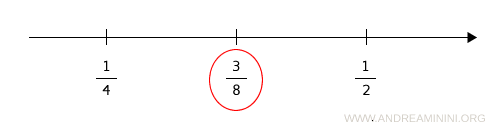
Between 3/8 and 1/2, there is again another midpoint.
$$ \frac{ \frac{3}{8} + \frac{1}{2} }{2} = \frac{ \frac{3+4}{8} }{2} = \frac{ \frac{7}{8} }{2} = \frac{7}{8} \cdot \frac{1}{2} = \frac{7}{16} $$
The rational number 7/16 lies at the same distance between 1/2 and 3/8.
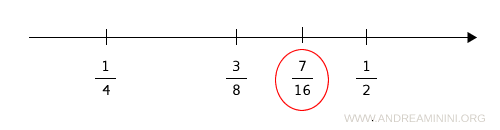
Continuing this process yields infinitely many points, each closer to 1/2 but never equal to 1/2.
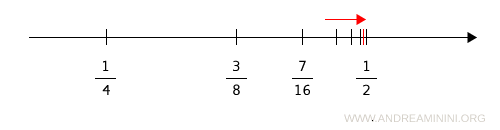
The same phenomenon occurs to the right of the point 1/2.
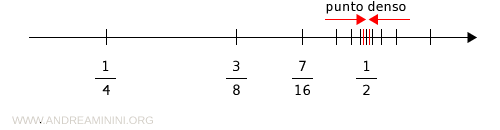
In this sense, the point 1/2 is called a dense point.
The same reasoning applies to every rational number. Every rational number is a dense point on the number line.
At this stage, one might be tempted to conclude that all points on the number line correspond to rational numbers, but this is not the case.
The set of rational numbers is infinite, and each rational number corresponds to one and only one point on the number line.
However, this correspondence does not work in reverse.
There exist points on the number line that are not rational numbers.
For example, the square root of 2 corresponds to a point on the line.
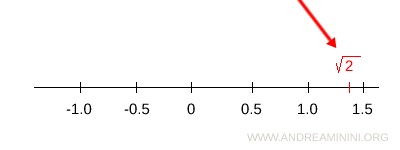
Nevertheless, there is no rational number equal to the square root of 2 (see the proof).
$$ \sqrt{2} \notin Q $$
Therefore, rational numbers are not sufficient to represent all points on a number line.
The line would still contain gaps, infinitely many gaps.
To fill these gaps, it is necessary to introduce another numerical set, the set of irrational numbers.
Difference Between Rational and Irrational Numbers
The set of rational numbers consists of terminating decimal numbers and repeating (periodic) decimal numbers. It does not include non-terminating, non-repeating decimal expansions.
The set of rational numbers is closed under the operations of addition, subtraction, multiplication, and division, with the sole exception of division by zero.
By contrast, the inverse operation of exponentiation, namely taking the square root or, more generally, the n-th root, is not an internal operation on the set of rational numbers.
In some cases, extracting a root produces a non-terminating, non-repeating decimal number.
Non-terminating, non-repeating decimal numbers are called irrational numbers because they do not belong to the set of rational numbers.
Example 4
The square root of 2 is a non-terminating, non-repeating decimal number.
$$ \sqrt{2} \notin Q $$
It is not a rational number because there exist no integers m and n whose ratio is equal to √2.
Example 5
Another example of a non-terminating, non-repeating decimal number is the number pi.
$$ 3.14159265358979323846... $$
Pi cannot be expressed as the ratio of two integers. Therefore, it is not a rational number.
Square Root in the Context of Rational Numbers
The square root is the inverse operation of squaring and is not an internal operation on the set of rational numbers.
The square root of a non-negative number n is a number m such that squaring m yields n.
$$ \sqrt{n} = m \Leftrightarrow m^2 = n $$
For example, the square root of 25 is equal to ±5.
$$ \sqrt{25} = \pm 5 $$
This is because there are two numbers, 5 and -5, whose squares are equal to 25.
$$ 5 \cdot 5 = 25 $$
$$ (-5) \cdot (-5) = 25 $$
Note. By convention, the principal (positive) square root is chosen, so $$ \sqrt{25} = 5 $$ When solving equations, however, both roots must be considered.
The square root of zero is zero.
$$ \sqrt{0} = 0 $$
The square root is not defined within the rational numbers for negative values.
Example. The square root of -25 does not exist within the rational numbers $$ \sqrt{-25} $$ because no real number squared yields a negative result.
Why is the square root not an internal operation on the rational numbers?
The square root fails to be an internal operation on the rational numbers because the square root of some rational numbers is not itself a rational number.
Example. The number 2 is a rational number $$ 2 \in Q $$ The square root of 2 exists, but it is not rational. See the proof. $$ \sqrt{2} \notin Q $$ The square root of 2 is an irrational number.
Rational Numbers and Points on the Number Line
Every rational number corresponds to a point on the number line, but not every point on the number line corresponds to a rational number.
The set of rational numbers is a dense but not complete set.
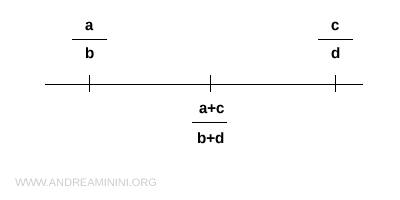
It is a dense set because, given two rational numbers a/b and c/d, it is always possible to find another rational number (a+b)/(c+d) lying strictly between them.
The set of rational numbers is not complete because it cannot be put into a one-to-one correspondence with the points on the number line.
Proof
Each rational number corresponds to a point on the number line.
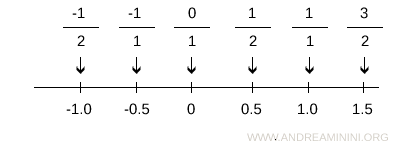
To show that not all points on the number line are rational numbers, it suffices to identify a point on the line that does not correspond to any rational number.
For example, the square root of two corresponds to a point on the number line but is not a rational number (see the proof).
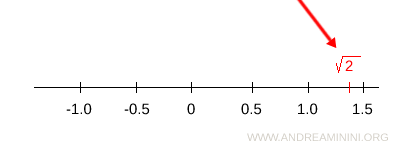
Note. Besides the square root of two, there are infinitely many other irrational points on the number line. For the purposes of this proof, however, exhibiting a single example is sufficient.
Therefore, the rational numbers form a proper subset of the points on the number line.
To obtain a one-to-one correspondence between a numerical set and the points on the number line, the numerical system must be extended to the set of real numbers.
And so on.
