Operations on rational numbers
Within the set of rational numbers Q, the following operations are defined.
Addition
The sum of two rational numbers expressed as fractions with the same denominator is a fraction with the same denominator and, as its numerator, the sum of the numerators. $$ \frac{a}{b} + \frac{c}{b} = \frac{a+c}{b} $$
Example. The sum of the rational numbers 3/2 and 5/2 $$ \frac{3}{2} + \frac{5}{2} = \frac{3+5}{2} = \frac{8}{2} $$
If the rational numbers have different denominators, I first reduce both fractions to a common denominator, and then add the numerators.
Example. The rational numbers 3/2 and 5/3 have different denominators. $$ \frac{3}{2} + \frac{5}{3} $$ The least common multiple of the denominators is mcm(2,3)=6. I apply the invariant property of fractions to rewrite them as two equivalent fractions with denominator 6. $$ \frac{3 \cdot 3}{2 \cdot 3} + \frac{5 \cdot 2}{3 \cdot 2} $$ $$ \frac{9}{6} + \frac{10}{6} $$ The fractions now share the same denominator, so I can add the numerators. $$ \frac{9}{6} + \frac{10}{6} = \frac{9+10}{6} = \frac{19}{6} $$
Addition is an internal operation on the set of rational numbers, since the sum of two rational numbers is always a rational number.
$$ a+b = c \ \in Q \ \ \ \forall \ a,b \in Q $$
Within the set of rational numbers, addition satisfies the commutative and associative properties.
$$ a+b=b+a \ \ \ \forall \ a,b \in Q $$
$$ a+(b+c)=(a+b)+c \ \ \ \forall \ a,b,c \in Q $$
The additive identity is zero, because adding zero to any rational number leaves it unchanged.
$$ a+0=0+a=a \ \ \ \forall \ a \in Q $$
For every rational number there exists an additive inverse such that the sum of the two numbers is equal to the additive identity, namely 0.
$$ a + (-a) = 0 $$
Example. The additive inverse of 2/3 is -2/3 $$ \frac{2}{3} - \frac{2}{3} = \frac{2-2}{3} = \frac{0}{3} = 0 $$
Subtraction
The subtraction of two rational numbers expressed as fractions with the same denominator yields a fraction with the same denominator and, as its numerator, the difference of the numerators. $$ \frac{a}{b} - \frac{c}{b} = \frac{a-c}{b} $$
Example. The difference between the rational numbers 5/2 and 3/2 $$ \frac{5}{2} - \frac{3}{2} = \frac{5-3}{2} = \frac{2}{2} = 1 $$
If the rational numbers have different denominators, I must first perform the reduction to a common denominator.
Once both fractions have been rewritten with the same denominator, I can compute the difference of the numerators.
Example. The rational numbers 5/2 and 2/3 have different denominators. $$ \frac{5}{2} - \frac{2}{3} $$ The least common multiple of the denominators is mcm(2,3)=6. I apply the invariant property of fractions to rewrite them as equivalent fractions with denominator 6. $$ \frac{5 \cdot 3}{2 \cdot 3} - \frac{2 \cdot 2}{3 \cdot 2} $$ $$ \frac{15}{6} - \frac{4}{6} $$ The fractions now have the same denominator, so I can subtract the numerators, that is, add the first numerator to the additive inverse of the second. $$ \frac{15}{6} - \frac{4}{6} = \frac{15-4}{6} = \frac{11}{6} $$
Subtraction is an internal operation on the set of rational numbers, since the difference of two rational numbers is always a rational number.
$$ a-b = c \ \in Q \ \ \ \forall \ a,b \in Q $$
Within the set of rational numbers, subtraction satisfies the invariant property.
Adding or subtracting the same rational number c to both the minuend a and the subtrahend b leaves the difference a-b unchanged.
$$ a-b = (a+c) - (b+c) \ \ \ \forall \ a,b,c \in Q $$
$$ a-b = (a-c) - (b-c) \ \ \ \forall \ a,b,c \in Q $$
Multiplication
The product of two rational numbers written as fractions is a fraction whose numerator is the product of the numerators and whose denominator is the product of the denominators. $$ \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} $$
Example. The product of 3/2 and 5/2 $$ \frac{3}{2} \cdot \frac{5}{2} = \frac{3 \cdot 5}{2 \cdot 2} = \frac{15}{4} $$
The product of equivalent fractions is always the same.
Example. The fractions 6/4 and 10/4 are equivalent to 3/2 and 5/2, respectively. Their product is therefore the same. $$ \frac{6}{4} \cdot \frac{10}{4} = \frac{6 \cdot 10}{4 \cdot 4} = \frac{60}{16} = \frac{15}{4} $$
Multiplication is an internal operation on the set of rational numbers, since the product of two rational numbers is always a rational number.
$$ a \cdot b = c \in Q \ \ \forall \ a,b \in Q $$
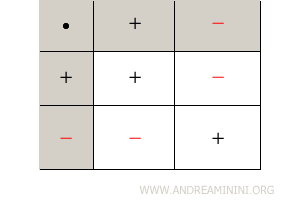
In the multiplication of rational numbers, the rules of signs for integers apply.
The product of two numbers with the same sign is positive, whereas the product of two numbers with opposite signs is negative.
Multiplication satisfies the commutative property.
$$ a \cdot b = b \cdot a $$
Example. The product of 5/2 and 3/4 is equal to the product of 3/4 and 5/2 $$ \frac{5}{2} \cdot \frac{3}{4} = \frac{3}{4} \cdot \frac{5}{2} = \frac{15}{8} $$
Multiplication satisfies the associative property.
$$ a \cdot (b \cdot c) = (a \cdot b) \cdot c $$
Example. A concrete example is $$ \frac{6}{4} \cdot \left( \frac{1}{2} \cdot \frac{2}{4} \right) = \left( \frac{6}{4} \cdot \frac{1}{2} \right) \cdot \frac{2}{4} $$
Multiplication satisfies the distributive property over addition.
$$ a \cdot (b + c) = a \cdot b + a \cdot c $$
Example. A concrete example is $$ \frac{6}{4} \cdot \left( \frac{1}{2} + \frac{2}{4} \right) = \frac{6}{4} \cdot \frac{1}{2} + \frac{6}{4} \cdot \frac{2}{4} $$
The multiplicative identity is the number 1, because multiplying any rational number by one leaves it unchanged.
$$ \forall \ a \in Q \Rightarrow a \cdot 1 = a $$
Example. The product of 4/3 and +1 is equal to 4/3. $$ \frac{4}{3} \cdot 1 = \frac{4 \cdot 1}{3 \cdot 1} = \frac{4}{3} $$
The absorbing element of multiplication is the number 0, because the product of any rational number and zero is zero.
$$ \forall \ a \in Q \Rightarrow a \cdot 0 = 0 $$
Consequently, in the multiplication of rational numbers, the zero product property holds.
Example. The product of 4/3 and 0 is equal to zero. $$ \frac{4}{3} \cdot 0 = \frac{4}{3} \cdot \frac{0}{1} = \frac{4 \cdot 0}{3 \cdot 1} = \frac{0}{3} = 0 $$ It is worth emphasizing a point that is often a source of confusion. Any integer n, when written as a fraction, is expressed as n/1. $$ n = \frac{n}{1} $$ Therefore, the number 0 written as a fraction is 0/1, not 0/0. $$ 0 = \frac{0}{1} $$
Any rational number multiplied by -1 is equal to its additive inverse, that is, the opposite element with respect to addition.
$$ \forall \ \frac{a}{b} \in Q , \ a,b \in Z \Rightarrow \frac{a}{b} \cdot (-1) = - \frac{a}{b} $$
Example. The product of 1/2 and -1 is equal to -1/2 $$ \frac{1}{2} \cdot (-1) = \frac{1}{2} \cdot \left( \frac{-1}{1} \right) = \frac{1 \cdot (-1)}{2 \cdot 1} = - \frac{1}{2} $$ Here, -1/2 is the additive inverse of 1/2 because their sum is equal to zero $$ \frac{1}{2} + \left( - \frac{1}{2} \right) = \frac{1}{2} - \frac{1}{2} = 0 $$
For every nonzero rational number there exists a multiplicative inverse, called the reciprocal, such that the product of the two numbers is equal to the multiplicative identity, namely 1.
$$ \frac{a}{b} \cdot \frac{b}{a} = 1 $$
Therefore, to find the reciprocal of a rational number, it is sufficient to interchange the numerator and the denominator.
Example. The reciprocal of 5/2 is the rational number 2/5 $$ \frac{5}{2} \cdot \frac{2}{5} = 1 $$
The only rational number without a multiplicative inverse is zero, because the reciprocal of zero would result in a division by zero, which is an undefined operation. $$ \frac{0}{1} \cdot \color{red}{ \frac{1}{0} } = impossible $$
Division
The division of two rational numbers, with the second one nonzero, yields a rational number called the quotient. It is defined as the product of the first number and the reciprocal of the second. $$ \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} $$
Example. The division of 5/2 by 3/2 is equal to 5/3 $$ \frac{\frac{5}{2}}{\frac{3}{2}} = \frac{5}{2} \cdot \frac{2}{3} = \frac{5}{3} $$
Division is the inverse operation of multiplication.
As a consequence, the same rules of signs that apply to multiplication also apply to division.

Division is an internal operation on the set of rational numbers, since the quotient of two rational numbers is again a rational number, provided that the divisor is nonzero.
$$ \forall \ n,m \in Q \ , \ m \ne 0 \Rightarrow \frac{n}{m} \in Q $$
Division is not defined when the divisor is equal to zero, because division by zero is an impossible operation in mathematics.
$$ \frac{n}{0} = \text{impossible} \ \ n \in Q $$
In the special case where both the numerator and the denominator are zero, the expression is undefined.
$$ \frac{0}{0} = \text{undefined} $$
Division of rational numbers satisfies the right distributive property with respect to addition.
$$ (n+m):p = n:p + m:p \ \ \ \ n,m,p \in Q $$
Example. The sum 5/2 + 3/2 divided by 1/2 is equal to the sum of the quotients 5/2 : 1/2 and 3/2 : 1/2 $$ \left( \frac{5}{2} + \frac{3}{2} \right) : \frac{1}{2} = \frac{5}{2} : \frac{1}{2} + \frac{3}{2} : \frac{1}{2} $$ Carrying out the algebraic steps on both sides yields the same result. $$ \frac{8}{2} : \frac{1}{2} = \frac{5}{2} \cdot \frac{2}{1} + \frac{3}{2} \cdot \frac{2}{1} $$ $$ \frac{8}{2} \cdot \frac{2}{1} = \frac{10}{2} + \frac{6}{2} $$ $$ \frac{16}{2} = \frac{16}{2} $$
Division does not satisfy a left distributive property with respect to addition.
$$ p:(n+m) \ne p:n + p:m $$
Example. The quotient of 1/2 by the sum 5/2 + 3/2 is not equal to the sum of the quotients 1/2 : 5/2 and 1/2 : 3/2 $$ \frac{1}{2} : \left( \frac{5}{2} + \frac{3}{2} \right) \ne \frac{1}{2} : \frac{5}{2} + \frac{1}{2} : \frac{3}{2} $$ Performing the algebraic steps on both sides produces different results. $$ \frac{1}{2} : \frac{8}{2} \ne \frac{1}{2} \cdot \frac{2}{5} + \frac{1}{2} \cdot \frac{2}{3} $$ $$ \frac{1}{2} \cdot \frac{2}{8} \ne \frac{1}{5} + \frac{1}{3} $$ $$ \frac{1}{8} \ne \frac{8}{15} $$
Division of rational numbers satisfies the invariant property.
If both the dividend and the divisor are multiplied or divided by the same nonzero rational number, the quotient remains unchanged.
$$ n:m = (n \cdot p):(m \cdot p) = (n : p):(m : p) \ \ \ \ n,m,p \in Q , \ p \ne 0 $$
Example. In the division of 5/2 by 3/2, multiply both the dividend and the divisor by 1/2 $$ \frac{5}{2} : \frac{3}{2} = \left( \frac{5}{2} \cdot \frac{1}{2} \right) : \left( \frac{3}{2} \cdot \frac{1}{2} \right) $$ Carrying out the algebraic steps on both sides yields the same result. $$ \frac{5}{2} \cdot \frac{2}{3} = \frac{5}{4} : \frac{3}{4} $$ $$ \frac{5}{3} = \frac{5}{4} \cdot \frac{4}{3} $$ $$ \frac{5}{3} = \frac{5}{3} $$ The same result is obtained if both the dividend and the divisor are divided by 1/2. $$ \frac{5}{2} : \frac{3}{2} = \left( \frac{5}{2} : \frac{1}{2} \right) : \left( \frac{3}{2} : \frac{1}{2} \right) $$ $$ \frac{5}{2} \cdot \frac{2}{3} = \left( \frac{5}{2} \cdot \frac{2}{1} \right) : \left( \frac{3}{2} \cdot \frac{2}{1} \right) $$ $$ \frac{5}{3} = \frac{5}{1} : \frac{3}{1} $$ $$ \frac{5}{3} = \frac{5}{1} \cdot \frac{1}{3} $$ $$ \frac{5}{3} = \frac{5}{3} $$
The identity element for division is the number 1, because dividing any rational number by one leaves it unchanged.
$$ \forall \ \frac{a}{b} \in Q , \ a,b \in Z \Rightarrow \frac{\frac{a}{b}}{1} = \frac{a}{b} $$
Here, 1 is an integer and can equivalently be written in fractional form as 1/1.
Example. The quotient of 1/2 and 1 is equal to 1/2 $$ \frac{1}{2} : 1 = \frac{1}{2} : \frac{1}{1} = \frac{1}{2} \cdot \frac{1}{1} = \frac{1}{2} $$
Therefore, any nonzero rational number divided by itself is equal to 1.
$$ \forall \ \frac{a}{b} \in Q , \ a,b \in Z \Rightarrow \frac{\frac{a}{b}}{\frac{a}{b}} = 1 $$
Example. The quotient of 1/2 and 1/2 is equal to 1 $$ \frac{1}{2} : \frac{1}{2} = \frac{1}{2} \cdot \frac{2}{1} = \frac{2}{2} = 1 $$
Any rational number divided by -1 is equal to its additive inverse, that is, its opposite with respect to addition.
$$ \forall \ \frac{a}{b} \in Q , \ a,b \in Z \Rightarrow \frac{\frac{a}{b}}{-1} = - \frac{a}{b} $$
Example. The quotient of 1/2 and -1 is equal to -1/2 $$ \frac{1}{2} : (-1) = \frac{1}{2} \cdot \frac{-1}{1} = - \frac{1}{2} $$ Here, -1/2 is the additive inverse of 1/2 because their sum is equal to zero $$ \frac{1}{2} + \left( - \frac{1}{2} \right) = 0 $$
The quotient of two rational numbers is not necessarily less than or equal to the dividend. It may also be greater than the dividend.
Example. The quotient of 5 and 1/2 is equal to 10, which is greater than the dividend (5). $$ 5 : \frac{1}{2} = \frac{5}{1} \cdot \frac{2}{1} = 10 $$
Exponentiation
The nth power of a rational number is equal to the nth power of the numerator divided by the nth power of the denominator. $$ \left( \frac{a}{b} \right)^n = \frac{a^n}{b^n} $$
For rational numbers, exponentiation can be interpreted as repeated multiplication of a number by itself.
Example. The fraction 2/5 raised to the third power is equal to 23/53 $$ \left( \frac{2}{5} \right)^3 = \frac{2}{5} \cdot \frac{2}{5} \cdot \frac{2}{5} = \frac{2 \cdot 2 \cdot 2}{5 \cdot 5 \cdot 5} = \frac{2^3}{5^3} $$
With respect to the sign, the same rule that governs multiplication applies.
Accordingly, the sign of a power depends on whether the exponent is an even or an odd integer.
- If the exponent is even, the power of any nonzero rational number is always positive.
- If the exponent is odd, the power is positive when the rational number is positive and negative when the rational number is negative.
Example. The power of the rational number 2/5 squared or cubed is always positive, since repeated multiplication involves a positive rational number. $$ \left( \frac{2}{5} \right)^2 = \frac{4}{25} $$ $$ \left( \frac{2}{5} \right)^3 = \frac{8}{125} $$ The power of the rational number -2/5 squared is positive, because multiplication is repeated an even number of times on a negative rational number. $$ \left( - \frac{2}{5} \right)^2 = \frac{4}{25} $$ Conversely, the power of the rational number -2/5 cubed is negative, because multiplication of a negative number by itself is repeated an odd number of times. $$ \left( - \frac{2}{5} \right)^3 = - \frac{8}{125} $$
The power of a nonzero rational number with a negative exponent is defined as the power whose base is the reciprocal of the given rational number and whose exponent is the additive inverse of the original exponent.
$$ \left( \frac{a}{b} \right)^{-n} = \left( \frac{b}{a} \right)^n $$
And so on.
