Hyperreal numbers

The hyperreal numbers are a number system that extends the real numbers (R) by introducing infinitely large numbers ∞ (infinite quantities) and infinitely small numbers ε (infinitesimals). This framework makes it possible to treat infinity and infinitesimal size in a precise and operational way.

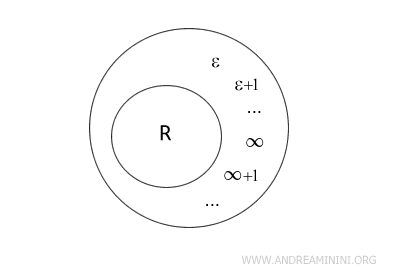
The set of hyperreal numbers is strictly larger than the set of real numbers (R), because it includes two additional and fundamentally new subclasses.

• Infinite numbers
  Infinite numbers are numbers that are greater than every real number, or smaller than every real number. They go beyond any finite bound. $$ \forall \ x \in R \ \Rightarrow \ \infty > x \ $$
• Infinitesimal numbers
  Infinitesimal numbers are smaller than every positive real number and greater than every negative real number. Intuitively, they are quantities that are nonzero yet smaller than any real magnitude. For this reason, infinitesimals can be viewed as reciprocals of infinite numbers, ε = 1/∞, and conversely. $$ \forall \ x \in R^+ \ \Rightarrow \ \epsilon < x \ $$

Although the set of hyperreal numbers is not a metric space, it is equipped with a topology that allows a well-defined ordering of hyperreal numbers.

Unlike the real numbers, within the hyperreal number system infinities are not merely symbolic placeholders. They behave as genuine numbers and can be compared and ordered.

$$ \infty < \infty + 1 < \infty +2 < ... $$

If ∞ is an infinite number, then ∞ + 1 is also infinite and is strictly greater than ∞.

The same idea applies to infinitesimal numbers, since they are defined as reciprocals of infinite numbers, ε = 1/∞.

$$ 0 < \epsilon < \epsilon + 1 < \epsilon +2 < ... $$

If ε is a nonzero infinitesimal, then it is smaller than ε + 1, and the ordering continues in the same way.

In short, infinity ∞ and the infinitesimal ε are treated as genuine numbers rather than as abstract symbols. As a result, they can be used directly as operands in algebraic and analytical calculations.

A practical example

Consider a straight line that is tangent to a circle at a single point.

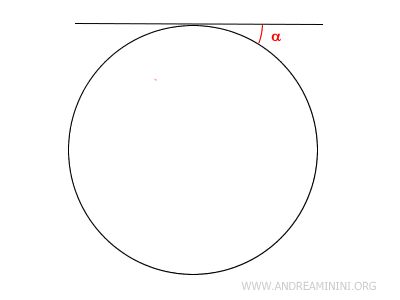
What is the angle between the tangent line and the circle?

The angle cannot be zero, because in that case the two sides of the angle would coincide.

At the same time, the angle cannot be strictly greater than zero, because then the line would intersect the circle and would no longer be tangent.

In situations like this, the angle between the tangent line and the circle is taken to be an infinitesimal (ε).

$$ \alpha = \epsilon $$

This example illustrates that the infinitesimal has a concrete mathematical role and is not merely a conceptual abstraction.

Nevertheless, in late nineteenth-century infinitesimal calculus, also known as standard analysis, the infinitesimal (ε) is not considered a real number. This is the framework developed by Karl Weierstrass and still used as the theoretical foundation of most university-level calculus courses.

During the twentieth century, some mathematicians began to ask whether infinitesimals should instead be treated as genuine numbers, rather than as purely formal tools.

This question led to the development of non-standard analysis.

Note. In non-standard analysis, the infinitesimal is a number and can be interpreted as the reciprocal of an infinitely large number in the denominator, $$ \epsilon = \frac{1}{\infty} $$ Consequently, if the infinitesimal is a number (ε), then infinity (∞) must also be a number. Since neither can be classified as a real number, they are grouped under the name hyperreal numbers. This numerical system is much larger and includes the real numbers (R), all infinitesimals (ε), and all infinite numbers (∞).

The field of hyperreal numbers

The hyperreal numbers form an ordered field, known as the field of hyperreal numbers.

The field of real numbers is a subfield of the field of hyperreal numbers.

Note. Hyperreal numbers are studied within non-standard mathematical analysis. The theory was introduced in 1966 by Abraham Robinson of Yale University in his book Non-Standard Analysis. Hyperreal numbers should not be confused with surreal numbers. While both systems offer rigorous ways to reason about infinite and infinitesimal quantities, they rely on different mathematical constructions and serve different purposes. See the difference between surreal and hyperreal numbers.

And so on.