Bounded Set in Metric Topology
In a metric space \((X, d)\), where \(d\) represents the metric that measures distances between points, a subset \(A \subseteq X\) is considered bounded if there exists a positive number \(\mu > 0\) such that the distance \(d(x, y)\) between any two points \(x, y \in A\) is always less than or equal to \(\mu\).
Simply put, all points in \(A\) are confined within a certain maximum distance \(\mu\) from one another.
If the entire set \(X\) is bounded with respect to the metric \(d\), we say that \(d\) is a bounded metric.
This implies that the distances between any pair of points in \(X\) are all less than some fixed maximum value \(\mu\).
Note: If the metric \(d\) is bounded, then every subset of \(X\) is automatically bounded, because no subset can have distances exceeding those of the whole set.
A Practical Example
Let’s consider the Cartesian plane \(\mathbb{R}^2\) with the Euclidean distance as the metric.
The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by the formula:
$$ d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
Now, take the subset \(A\) of \(\mathbb{R}^2\), defined as all points \((x, y)\) that satisfy the equation of a circle with a radius of \(10\), centered at the origin. This subset \(A\) is described by:
$$ A = \{(x, y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 10^2\} $$
A set is bounded if there exists a value \(\mu > 0\) such that, for every pair of points \((x_1, y_1), (x_2, y_2) \in A\), we have \(d((x_1, y_1), (x_2, y_2)) \leq \mu\).
In \(A\), the greatest possible distance between two points occurs when they lie on opposite ends of the circle’s diameter (e.g., \((10, 0)\) and \((-10, 0)\)).
The distance between these points is:
$$ d((10, 0), (-10, 0)) = \sqrt{((-10) - 10)^2 + (0 - 0)^2} = \sqrt{(-20)^2} = 20 $$
Thus, the maximum distance between any two points in \(A\) is \(20\).
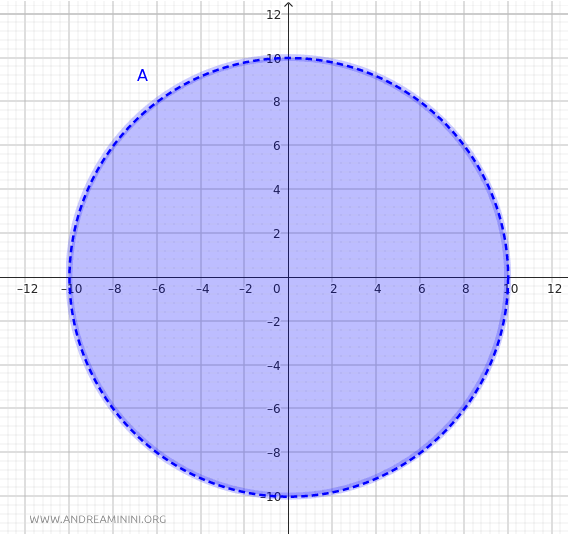
This means that no matter which two points you select within the circle, their distance will never exceed \(20\).
Therefore, the set \(A\) is bounded with \(\mu = 20\), as all points \((x, y) \in A\) are contained within a maximum distance—the circle’s diameter.
The Bound of a Metric Does Not Affect Topology
It’s important to note that whether a metric is bounded or not does not affect the topology it induces—that is, the way open and closed sets are structured.
What is topology? Topology is a way of defining what it means for a set to be "open" or "closed." It doesn’t depend on the exact numerical values of the metric but on the overall structure of the space.
Therefore, even if a metric is unbounded, we can always find an equivalent bounded metric that preserves the exact same topology.
In other words: Whether a metric is bounded or not does not change how open or closed sets are defined in the space.
Example
To transform an unbounded metric into a bounded one, we can apply a mathematical function that "compresses" large distances without altering the topology of the space.
A common method involves using a transformation like this:
$$ d'(x, y) = \frac{d(x, y)}{1 + d(x, y)} $$
How does this transformation work?
When the distance \(d(x, y)\) is small, \(d'(x, y)\) closely approximates \(d(x, y)\).
For instance, if \(d(x, y) = 1\), the new distance becomes:
$$ d'(x, y) = \frac{1}{1 + 1} = 0.5 $$
When \(d(x, y)\) is very large (approaching infinity), the new distance \(d'(x, y)\) approaches \(1\).
In this way, no matter how large the original distances are, this transformation ensures all distances fall within the range of 0 to 1.
For example, consider a metric space \((X, d)\) where the distance is defined as \(d(x, y) = |x - y|\) (the standard Euclidean metric).
This metric is unbounded, as \(x\) and \(y\) can be arbitrarily far apart.
Applying the transformation gives:
$$ d'(x, y) = \frac{|x - y|}{1 + |x - y|} $$
If \(x = 1\) and \(y = 2\), the original distance is \(d(1, 2) = 1\), while the transformed distance becomes:
$$ d'(1, 2) = \frac{1}{1 + 1} = 0.5 $$
If \(x = 1\) and \(y = 1000\), the original distance is \(d(1, 1000) = 999\), but the transformed distance becomes:
$$ d'(1, 1000) = \frac{999}{1 + 999} = 0.999 $$
As a result, all distances are confined to the range of 0 to 1.
The structure of the space remains unchanged because the open and closed sets defined by \(d\) and \(d'\) are identical.
And so forth.
