Chi-Square
The chi-square test (χ²) is a statistical tool used to determine whether there's a significant difference between observed and expected frequencies across one or more categories.
The chi-square test is primarily applied in two scenarios:
- Test of Independence: Used to determine whether two categorical variables are independent. For example, it could be used to check if there's a relationship between gender (male/female) and preference for a product type (A/B).
- Goodness of Fit Test: Used to compare observed frequencies with those expected based on a theoretical distribution. For example, it can help determine if the results of rolling a die are evenly distributed.
Overall, it's a powerful tool for testing whether two categorical variables are independent or for comparing observed data to a theoretical distribution.
Note. The chi-square test is also known as the Pearson’s chi-square test, named after statistician Karl Pearson, who developed it to analyze relationships between variables. Sometimes it's referred to as the Pizzetti-Pearson test, recognizing the contributions of another statistician, Paolo Pizzetti. When used specifically to test for independence between two categorical variables, it's often called the Test of Independence.
How to Calculate the Chi-Square
The chi-square value is calculated using the following formula:
$$ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} $$
Where:
- \( O_i \) represents the observed frequencies in each category.
- \( E_i \) represents the expected frequencies based on the null hypothesis, which usually assumes the independence of the variables or follows a specific theoretical distribution.
If the value of \( \chi^2 \) is large, it indicates a significant difference between the observed and expected frequencies.
How to Interpret the Chi-Square Value
To interpret the result, compare the calculated \( \chi^2 \) value with a critical value \( \chi^2_{\alpha, df} \), found in a chi-square distribution table.
- If the calculated \( \chi^2 \) exceeds the critical value, this suggests the variables are dependent or the observed distribution differs from the expected one, leading to rejection of the null hypothesis (independence).
- If the calculated \( \chi^2 \) is lower than the critical value, the variables might be independent, as there’s not enough evidence to claim that the variables are associated or that the observed distribution deviates from the expected one. In this case, the null hypothesis cannot be rejected.
The critical value is typically denoted \( \chi^2_{\alpha, df} \), where:
- \( \alpha \) represents the significance level (e.g., 0.05 or 0.01). This sets the threshold for accepting or rejecting a hypothesis, based on the probability of error you're willing to accept.
For example, a significance level of α=0.05 means you're willing to accept a 5% chance of making a Type I error—in other words, there's a 5% risk that the result might be due to chance.
- \( df \) represents the degrees of freedom in the test. The degrees of freedom are based on the dimensions of the contingency table used for data analysis: $$ df = (r - 1) \times (c - 1) $$ where $ r $ is the number of rows and $ c $ is the number of columns in the table. Degrees of freedom reflect the possible combinations between the categories of the two variables in the contingency table.
For example, in a table with r=2 rows and c=3 columns, the degrees of freedom are df=2. $$ df = (2 - 1) \times (3 - 1) = 2 $$
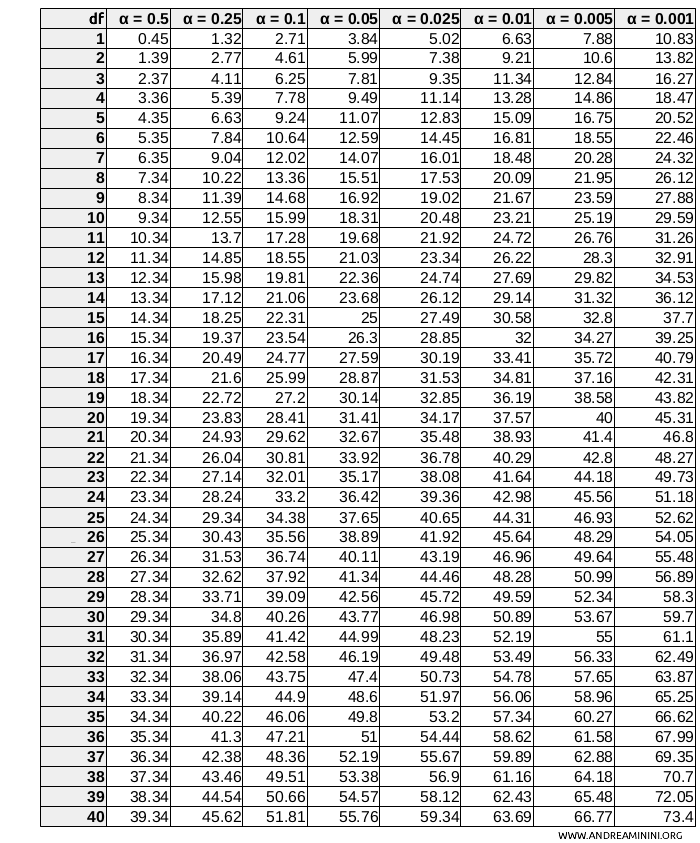
To find the critical value, consult the chi-square distribution table.
For example, \( \chi^2_{0.05, 2} \) represents the critical value for a 5% significance level (α=0.05) and 2 degrees of freedom. You can find this value by locating the row for $ df=2 $ and the column for $ \alpha=0.05 $. In this case, the critical value is \( \chi^2_{0.05, 2} = 5.99 \).
A Practical Example
I want to check if there's a relationship between gender (Male/Female) and snack preference (A, B, or C).
I surveyed 100 people and collected the following data:
| Snack A | Snack B | Snack C | Total | |
|---|---|---|---|---|
| Male | 20 | 15 | 10 | 45 |
| Female | 10 | 25 | 20 | 55 |
| Total | 30 | 40 | 30 | 100 |
The table shows the observed frequencies for snack preferences and gender.
It has $ r=2 $ rows and $ c=3 $ columns, excluding the total counts.
Note. The contingency table used in the chi-square test is also referred to as a contingency table. "Contingency" means the relationship or dependency between two or more variables. Essentially, it indicates that the occurrence of one variable may be associated with the occurrence of another. This table shows the joint frequencies of the categories of two variables and can include both observed and expected frequencies.
First, I need to calculate the expected frequencies (\( E_{ij} \)) using this formula:
$$ E_{ij} = \frac{(\text{Row Total}) \times (\text{Column Total})}{\text{Grand Total}} $$
Expected frequencies are the frequencies we would expect to see if the variables were independent.
I calculate the expected frequencies for each cell in the table:
- Male, Snack A $$ E_{11} = \frac{(45) \times (30)}{100} = 13.5 $$
- Male, Snack B $$ E_{12} = \frac{(45) \times (40)}{100} = 18 $$
- Male, Snack C $$ E_{13} = \frac{(45) \times (30)}{100} = 13.5 $$
- Female, Snack A $$ E_{21} = \frac{(55) \times (30)}{100} = 16.5 $$
- Female, Snack B $$ E_{22} = \frac{(55) \times (40)}{100} = 22 $$
- Female, Snack C $$ E_{23} = \frac{(55) \times (30)}{100} = 16.5 $$
The contingency table with expected frequencies is as follows:
| Snack A | Snack B | Snack C | Total | |
|---|---|---|---|---|
| Male | 13.5 | 18 | 13.5 | 45 |
| Female | 16.5 | 22 | 16.5 | 55 |
| Total | 30 | 40 | 30 | 100 |
Once I’ve calculated all the expected frequencies, I apply the chi-square formula:
$$ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} $$
Where \( O_{ij} \) are the observed frequencies from the survey and \( E_{ij} \) are the expected ones.
I calculate each term in the sum:
- Male, Snack A $$ \frac{(20 - 13.5)^2}{13.5} = \frac{6.5^2}{13.5} \approx 3.13 $$
- Male, Snack B $$ \frac{(15 - 18)^2}{18} = \frac{(-3)^2}{18} \approx 0.5 $$
- Male, Snack C $$ \frac{(10 - 13.5)^2}{13.5} = \frac{(-3.5)^2}{13.5} \approx 0.91 $$
- Female, Snack A $$ \frac{(10 - 16.5)^2}{16.5} = \frac{(-6.5)^2}{16.5} \approx 2.56 $$
- Female, Snack B $$ \frac{(25 - 22)^2}{22} = \frac{3^2}{22} \approx 0.41 $$
- Female, Snack C $$ \frac{(20 - 16.5)^2}{16.5} = \frac{3.5^2}{16.5} \approx 0.74 $$
Then, I sum all the terms:
$$ \chi^2 = 3.13 + 0.5 + 0.91 + 2.56 + 0.41 + 0.74 $$
The final result is the chi-square value \( \chi^2 = 8.25 \).
$$ \chi^2 = 8.25 $$
To interpret the chi-square value, I compare it with a critical value from the chi-square distribution.
In this case, the contingency table has $ df=2 $ degrees of freedom because it has two rows ( $ r=2 $) and three columns ( $ c=3 $ ).
$$ df = (r - 1) \times (c - 1) $$
$$ df = (2 - 1) \times (3 - 1) $$
$$ df = 2 $$
I select a significance level of \( \alpha = 0.05 \), meaning there's a 5% chance that the result is due to randomness or error.
Looking at the chi-square table, I find the critical value for $ df = 2 $ degrees of freedom and a significance level \( \alpha = 0.05 \).
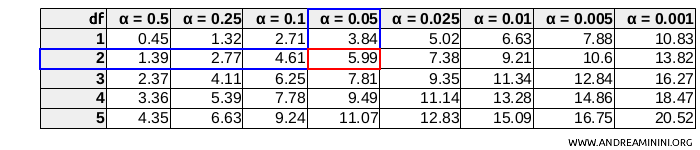
In this case, the critical value is approximately 5.99.
$$ \chi^2_{0.05, 2} = 5.99 $$
Finally, I compare the chi-square value I calculated ($ \chi^2 = 8.25 $) with the critical value ($ \chi^2_{0.05, 2} = 5.99 $).
- If $ \chi^2 > \chi^2_{0.05, 2} $, the variables are dependent.
- If $ \chi^2 \le \chi^2_{0.05, 2} $, the variables may be independent.
Since \( \chi^2 = 8.25 \) is greater than \( \chi^2_{0.05, 2} = 5.99 \), I conclude that the variables are not independent, suggesting a significant relationship between gender (Male/Female) and snack preference (A, B, or C).
This result leads me to reject the null hypothesis (independence between the two variables).
In other words, the two variables are dependent.
Note. On the other hand, if the chi-square value had been less than or equal to the critical value, ($ \chi^2 \le \chi^2_{0.05, 2} $), I would have accepted the null hypothesis (independence of the variables), indicating that snack preferences are not influenced by gender.
Additional Notes
Some additional notes and observations regarding the Chi-Square Test:
- The Chi-Square Test is only applicable to categorical data, not continuous quantitative data
The Chi-Square Test is specifically for categorical (qualitative) data, like gender (male/female), eye color (light/dark), or product preference (A, B, C). It is not suitable for continuous quantitative data, such as height, weight, or temperature, which require different statistical tests, such as the t-test or ANOVA, designed to compare means and variances of continuous data.Note. The reason is that the Chi-Square Test assesses the frequency of observations in each category and compares these to the expected frequencies, assuming the data are counted and not measured on a continuous scale.
- Expected frequencies should be sufficiently large
Expected frequencies in each category should be sufficiently large (generally at least 5) to ensure reliable results. If expected frequencies are too low, the chi-square calculation may become inaccurate, and the distribution may not align well with expected values, leading to incorrect conclusions. A common rule of thumb is that the expected frequencies in each cell of the contingency table should be at least 5.
Note. When many cells have expected frequencies below 5, a possible approach is to combine categories to increase frequencies in each cell. Alternatively, a different test like Fisher’s exact test may be more appropriate for low-frequency scenarios.
And so forth.
