Pearson Correlation Coefficient

The Pearson correlation coefficient, \( r \), measures the linear relationship between two variables. $$ r = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} $$ where \( X \) and \( Y \) are the observed variables, and \( \bar{X} \) and \( \bar{Y} \) are their respective means.

The Pearson coefficient is also known as the Bravais-Pearson correlation coefficient.

This coefficient is dimensionless, meaning it’s unaffected by the units or scale of the variables involved.

The Pearson coefficient ranges from -1 to 1, where:

• r = 1 indicates a perfect positive (or direct) correlation; as one variable increases, the other rises proportionally.
• r = -1 represents a perfect negative (or inverse) correlation; as one variable increases, the other decreases proportionally.
• r = 0 indicates no linear correlation between the variables.

It’s important to note that Pearson’s coefficient only measures linear correlation between two variables. It doesn’t capture other types of relationships, such as quadratic, exponential, or curved correlations.

When variables are linked in a non-linear way, the Pearson coefficient may appear low or even zero, even if a strong relationship exists between them.

Correlation doesn’t imply causation. A high correlation doesn’t necessarily mean that one variable causes the other; both might depend on a third factor. Likewise, a lack of correlation doesn’t rule out causation—there could be a hidden causal relationship affected by non-linear factors. Correlation reflects a statistical link, while causation suggests a direct effect of one variable on the other.

An Example in Practice

Let’s consider a simple dataset with two variables: hours of study (X) and exam scores (Y).

The data collected from five students is shown below:

Student	Study Hours (X)	Score (Y)
A	2	50
B	3	60
C	5	80
D	7	85
E	9	95

Note. This example uses data from only five students, which is a very small sample and may not be representative. However, it helps illustrate the calculation process. Generally, a larger sample provides a clearer view of the correlation between study hours and academic performance.

Calculating the means of the two variables \( X \) and \( Y \):

$$ \bar{X} = \frac{2 + 3 + 5 + 7 + 9}{5} = 5.2 $$

$$ \bar{Y} = \frac{50 + 60 + 80 + 85 + 95}{5} = 74 $$

For each \( X \) and \( Y \) value, calculate the deviations from the mean, \( X - \bar{X} \) and \( Y - \bar{Y} \), and the products of these deviations \( (X - \bar{X})(Y - \bar{Y}) \).

We also square these deviations to get \( (X - \bar{X})^2 \) and \( (Y - \bar{Y})^2 \).

Student	\( X \)	\( Y \)	\( X - \bar{X} \)	\( Y - \bar{Y} \)	\( (X - \bar{X})(Y - \bar{Y}) \)	\( (X - \bar{X})^2 \)	\( (Y - \bar{Y})^2 \)
A	2	50	-3.2	-24	76.8	10.24	576
B	3	60	-2.2	-14	30.8	4.84	196
C	5	80	-0.2	6	-1.2	0.04	36
D	7	85	1.8	11	19.8	3.24	121
E	9	95	3.8	21	79.8	14.44	441

Now, sum the values in the final columns:

$$ \sum (X - \bar{X})(Y - \bar{Y}) = 206 $$

$$ \sum (X - \bar{X})^2 = 32.8 $$

$$ \sum (Y - \bar{Y})^2 = 1370 $$

Using these, we calculate Pearson’s coefficient \( r \)

$$ r = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \cdot \sum{(Y - \bar{Y})^2}}} $$

Substituting the values, we get:

$$ r = \frac{206}{\sqrt{32.8 \cdot 1370}} \approx 0.97$$

This result, \( r \approx 0.97 \), shows a strong positive correlation between study hours and exam scores.

This suggests that more hours of study are associated with higher grades.

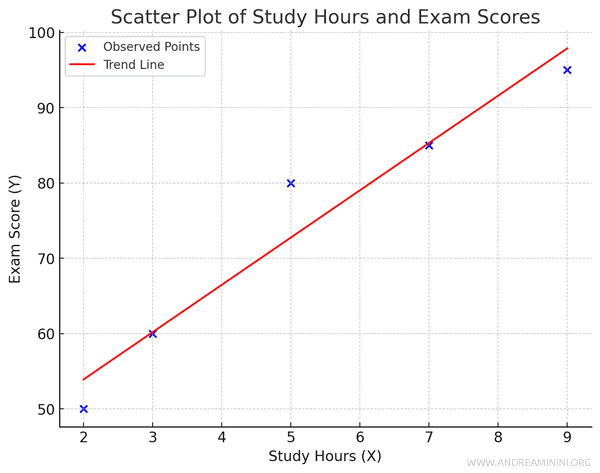
Note. Although there is a strong correlation, this does not imply causation. External factors, such as study quality or individual ability, can also impact scores. Simply increasing study hours does not guarantee better grades, as study methods play a critical role.

Calculating the Correlation Coefficient Using Regression Coefficients

Pearson’s correlation coefficient \( r \) can also be found as the square root of the product of the regression coefficients \( m \) and \( m_1 \) of the regression lines: $$ r = \pm \sqrt{m \cdot m_1} $$

This formula is based on the fact that the product of regression coefficients equals the square of the correlation coefficient, \( r^2 \).

The sign of \( r \) depends on the signs of \( m \) and \( m_1 \):

• If both regression coefficients are positive, \( r \) will be positive.
• If both are negative, \( r \) will be negative.

So, by knowing the regression coefficients (or slopes) of the regression lines, we can determine the Pearson correlation coefficient between the two variables.

Proof

Suppose we know the regression coefficients of \( X \) and \( Y \)

$$ m_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2} $$

$$ m_2 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (y_i - \bar{y})^2} $$

We calculate the product \( m \cdot m_1 \) of the regression coefficients:

$$ m \cdot m_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2} \cdot \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (y_i - \bar{y})^2} $$

$$ m \cdot m_1 = \frac{\left[\sum (x_i - \bar{x})(y_i - \bar{y})\right]^2}{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2} $$

This result equals the square of Pearson’s linear correlation coefficient.

$$ m \cdot m_1 = r^2 $$

Thus, the Pearson coefficient is the square root of the product of the regression coefficients.

$$ r = \pm \sqrt{m \cdot m_1}. $$

The sign of \( r \) is determined by the signs of the regression coefficients.

• The coefficient \( r \) is positive if both coefficients are positive.
• The coefficient \( r \) is negative if both coefficients are negative.

This demonstrates the relationship between the Pearson coefficient and the regression coefficients.

Relationship Between Pearson’s Coefficient, Regression Coefficients, and Standard Deviation

Given that Pearson’s coefficient is:

$$ r = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} $$

The standard deviations are:

$$ \sigma_X = \sqrt{ \frac{1}{n} \cdot \sum (X - \bar{X})^2 } $$

$$ \sigma_Y = \sqrt{ \frac{1}{n} \cdot \sum (Y - \bar{Y})^2 } $$

Multiplying Pearson’s coefficient by the ratio of the standard deviations:

$$ m_1 = r \frac{\sigma_Y}{\sigma_X} $$

$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} \cdot \frac{ \sqrt{ \frac{1}{n} \cdot \sum (X - \bar{Y})^2 } }{ \sqrt{ \frac{1}{n} \cdot \sum (Y - \bar{X})^2 } } $$

$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} \cdot \sqrt{ \frac{1}{n} \cdot \sum (Y - \bar{Y})^2 \cdot \frac{n}{ \sum (X - \bar{X})^2 } } $$

$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} \sum{(Y - \bar{Y})^2}}} \cdot \sqrt{ \frac{ \sum (Y - \bar{Y})^2 }{ \sum (X - \bar{X})^2 } } $$

$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} } \cdot \sqrt{ \sum{(Y - \bar{Y})^2}}} \cdot \frac{ \sqrt{ \sum (Y - \bar{Y})^2 } }{ \sqrt{ \sum (X - \bar{X})^2 }} $$

$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{\sqrt{\sum{(X - \bar{X})^2} } \cdot \sqrt{ \sum (X - \bar{X})^2 } } $$

$$ m_1 = \frac{\sum{(X - \bar{X})(Y - \bar{Y})}}{ \sum{(X - \bar{X})^2} } $$

This yields the regression coefficient of \( Y \) relative to \( X \), where $ y = m_1 x + q_1 $

Note. Following the same approach, we can show that the regression coefficient of \( X \) relative to \( Y \), where $ x = m_2 y + q_2 $, is $$ m_2 = r \frac{\sigma_X}{\sigma_Y} $$ Simply invert the standard deviation ratio and continue with the algebraic simplifications.

Pros and Cons of Pearson’s Coefficient

Pearson’s coefficient has some notable limitations:

• Only detects linear relationships
  It captures only linear relationships between two variables, overlooking any non-linear connections. For quadratic, exponential, or curvilinear relationships, Pearson may give misleading results. In these cases, alternative measures, like Spearman’s coefficient, or specific curve analysis may be more appropriate.
• Sensitive to outliers
  Outliers can significantly affect the result, potentially distorting the real relationship in the data.
• Requires continuous, quantitative variables
  Pearson works only with interval or ratio scales. For categorical or ordinal variables, methods like Spearman’s correlation are preferred.
• Assumes normal distribution
  Pearson’s correlation works best with normally distributed data. Without this, interpreting the coefficient can be less reliable.
• Doesn’t imply causation
  Like all correlation measures, Pearson’s coefficient doesn’t imply causation; a strong correlation doesn’t mean one variable causes the other.

However, Pearson’s coefficient also offers distinct advantages:

• Easy to interpret
  Ranging between -1 and 1, extreme values indicate a perfect linear correlation, making it easy to understand the strength and direction of a relationship.
• Quick to calculate
  Pearson’s coefficient is relatively simple to compute, making it a convenient choice for exploratory analysis.
• Sensitive to linear changes
  It’s particularly useful for measuring and comparing linear relationships between continuous variables.
• Useful for preliminary analysis
  It provides an initial insight into potential relationships, guiding further, in-depth analysis if necessary.

And so forth.