Statistical Dependence and Independence
In statistics, dependence between two variables refers to a relationship where changes in one variable influence or are associated with changes in another.
When two variables are dependent, the categories of one affect the distribution of the categories of the other.
Put simply, knowing the value or category of one variable helps to predict or explain the value or category of the other.
For instance, if I'm looking at gender (male or female) and preferred reading type (novel, essay, mystery) among a group of people, I would say there's dependence if reading preferences significantly differ based on gender.
On the other hand, if reading preferences remain the same regardless of gender, we would call that independence between the two variables.
To assess the dependence or independence between two variables, I can use statistical tests like the Chi-square (\(\chi^2\)) test.
This test compares the observed frequencies (collected data) with the expected frequencies under the assumption of complete independence.
What are expected frequencies? Expected frequencies are the values we expect to observe if the variables are independent. They allow us to compare the observed data and determine if there is a significant relationship.
A Practical Example
In this example, I consider a group of 100 students and aim to check if there's a dependence between gender (male or female) and their preferred subject (math or literature).
I collect the data and create a contingency table.
| Math | Literature | Total | |
|---|---|---|---|
| Male | 30 | 20 | 50 |
| Female | 10 | 40 | 50 |
| Total | 40 | 60 | 100 |
This table shows the absolute frequencies of the data collected.
Now, to determine if there is a dependence between gender and subject preference, I need to calculate the expected frequencies, assuming the two variables are independent.
The expected frequencies are calculated by multiplying the row total by the column total and dividing by the overall total:
- Math and males $$ \frac{50 \cdot 40}{100} = 20 $$
- Literature and males $$ \frac{50 \cdot 60}{100} = 30 $$
- Math and females $$ \frac{50 \cdot 40}{100} = 20 $$
- Literature and females $$ \frac{50 \cdot 60}{100} = 30 $$
I then replace the absolute frequencies (in red) with the expected frequencies in the contingency table.
| Math | Literature | Total | |
|---|---|---|---|
| Male | 20 | 30 | 50 |
| Female | 20 | 30 | 50 |
| Total | 40 | 60 | 100 |
Now, comparing the observed frequencies (in parentheses) with the expected frequencies (in red), we can already see that the observed frequencies differ quite significantly from the expected ones.
| Math | Literature | Total | |
|---|---|---|---|
| Male | 20 (30) | 30 (20) | 50 |
| Female | 20 (10) | 30 (40) | 50 |
| Total | 40 | 60 | 100 |
For example, it's evident that males show a stronger preference for math than expected (30 vs. 20), while females prefer literature more than expected (40 vs. 30).
This difference suggests there is a statistical dependence between gender and subject preference. In other words, preferences for math or literature vary depending on gender.
The Chi-Square Test
To measure this dependence statistically, I can apply the Chi-square (\(\chi^2\)) test.
If the test result is significant, it confirms the existence of a relationship between the two variables, indicating they are not independent.
The formula for calculating the Chi-square value is:
$$ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} $$
Where \(O_{ij}\) are the observed frequencies, and \(E_{ij}\) are the expected frequencies calculated earlier.
The difference between the observed and expected frequency, \( O_{ij} - E_{ij} \), is known as contingency.
I calculate \(\chi^2\) for each cell:
- Math and males $$ \frac{(30 - 20)^2}{20} = \frac{100}{20} = 5 $$
- Literature and males $$ \frac{(20 - 30)^2}{30} = \frac{100}{30} \approx 3.33 $$
- Math and females $$ \frac{(10 - 20)^2}{20} = \frac{100}{20} = 5 $$
- Literature and females $$ \frac{(40 - 30)^2}{30} = \frac{100}{30} \approx 3.33 $$
I sum all the results obtained:
$$ \chi^2 = 5 + 3.33 + 5 + 3.33 = 16.67 $$
The Chi-square value is therefore \(16.67\).
Note. The Chi-square value increases with the amount of observed data. To avoid this issue, a normalized Chi-square is often used: $$ C = \frac{\chi^2}{N \cdot (h-1)} $$ Where \(N\) is the number of observations, and \(h\) is the smaller number between the rows and columns in the table. In this case, \(N=100\) as there are 100 students surveyed, and \(h=2\), so the normalized Chi-square is: $$ C = \frac{16.67}{100 \cdot (2-1)} = \frac{16.67}{100} = 0.1667 $$ Alternatively, I could calculate the mean square contingency index: $$ I_c = \sqrt{ \frac{ \chi^2 }{ \chi^2 + N } } = \sqrt{ \frac{16.67}{16.67+100} } = \sqrt{0.1427} = 0.377 8 $$
Finally, I compare this value with the critical value of the Chi-square distribution with 1 degree of freedom (given by \((2-1) \times (2-1)\)) to determine if there is a significant dependence between the variables.
Critical Value of the Chi-Square Distribution and Degrees of Freedom
When calculating the Chi-square value, to determine if it is significant, it is compared with a critical value from a Chi-square distribution.
This critical value depends on:
- the chosen significance level (usually \( \alpha = 0.05 \), corresponding to a 5% probability)
- the degrees of freedom of the test.
The degrees of freedom (\(df\)) for a contingency table are calculated as:
$$ df = (\text{number of rows} - 1) \times (\text{number of columns} - 1) $$
In this example, there are 2 rows (Male and Female) and 2 columns (Math and Literature). Therefore:
$$ df = (2 - 1) \times (2 - 1) = 1 $$
For \(df = 1\) and \( \alpha = 0.05 \), the critical value is approximately 3.841.
Note. The value 3.841 is derived from the Chi-square distribution ( \( \chi^2 \) ) corresponding to a 5% significance level (or \( \alpha = 0.05 \) ) with 1 degree of freedom. There are standard Chi-square distribution tables that provide critical values for various degrees of freedom and significance levels.
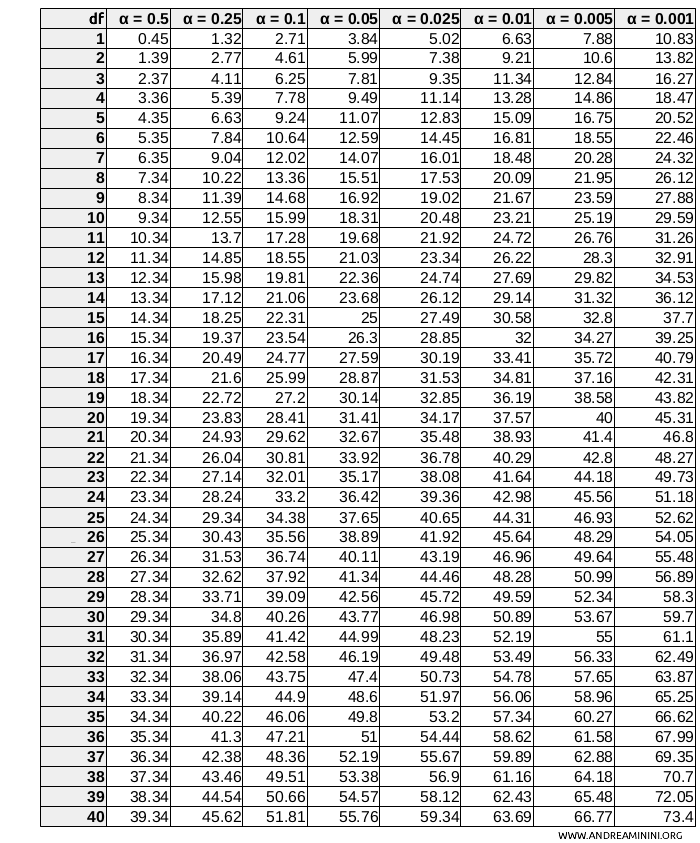
Finally, I compare the Chi-square value \(16.67\) with the critical value obtained from the table:
- If the \( \chi^2 \) value is greater than 3.841, there is a significant dependency between the variables.
- If the \( \chi^2 \) value is less than or equal to 3.841, the variables are independent.
In this case, the calculated value \( \chi^2 = 16.67 \) is greater than the critical value
$$ 16.67 > 3.841 $$
This indicates that there is a significant dependency between gender and subject preference, confirming they are not independent.
And so forth.
