Correlation in statistics
Correlation in statistics measures the relationship between two or more variables, showing whether and how they change together. When variables move in the same direction, it’s called positive correlation; when they move in opposite directions, it’s called negative correlation.
To measure the correlation between two variables, I can use the covariance.
Covariance gives a positive or negative value, indicating whether there is a positive or negative correlation between the data.
- Positive Correlation
If the covariance is positive, the two variables are positively correlated: when one increases, the other tends to increase as well. - Negative Correlation
If the covariance is negative, the variables are negatively correlated: when one increases, the other tends to decrease.
However, covariance is not a standardized measure because it depends on the unit of measurement of the data, making it difficult to interpret its absolute value.
For this reason, correlation is often measured using the Pearson correlation coefficient, which takes standardized values between -1 and 1, where:
- 1 indicates perfect positive correlation,
- 0 indicates no correlation,
- -1 indicates perfect negative correlation.
Note: Correlation should not be confused with causation. Two variables may move together without having a cause-and-effect relationship.
A Practical Example
In this example, let’s consider two variables \( X \) and \( Y \):
$$ X = [1, 2, 3, 4, 5] $$
$$ Y = [2, 4, 6, 8, 10] $$
To measure correlation, I calculate both the covariance and the Pearson correlation coefficient.
First, I find the mean of each variable:
$$ \bar{X} = \frac{1 + 2 + 3 + 4 + 5}{5} = 3 $$
$$ \bar{Y} = \frac{2 + 4 + 6 + 8 + 10}{5} = 6 $$
Next, I calculate the covariance. The formula for covariance between two variables \( X \) and \( Y \) is:
$$ \text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y}) $$
Where \( n \) is the number of pairs (in this case \( n = 5 \)).
Let’s calculate the individual products:
| $ X_i $ | $ Y_i $ | $ (X_i - \bar{X})(Y_i - \bar{Y}) $ | Result |
|---|---|---|---|
| 1 | 2 | (1−3)(2−6) | 8 |
| 2 | 4 | (2−3)(4−6) | 2 |
| 3 | 6 | (3−3)(6−6) | 0 |
| 4 | 8 | (4−3)(8−6) | 2 |
| 5 | 10 | (5−3)(10−6) | 8 |
Now I sum the products to find the covariance:
$$ \text{Cov}(X, Y) = \frac{8 + 2 + 0 + 2 + 8}{5} $$
$$ \text{Cov}(X, Y) = \frac{20}{5} = 4.0 $$
The covariance is 4.0, which suggests a positive correlation between the variables.
But covariance only tells us if two variables tend to move together, it doesn’t directly measure correlation.
Note: Covariance shows whether two variables tend to move in the same direction (positive covariance) or in opposite directions (negative covariance), but it isn’t standardized, so its absolute value can be hard to interpret.
To get a clearer, more interpretable value, I also calculate the Pearson correlation coefficient, which is a normalized version of covariance.
The Pearson coefficient ranges from -1 to 1, giving a more precise measure of the linear relationship between the variables.
The formula is:
$$ r = \frac{\text{Cov}(X, Y)}{\sigma_X \cdot \sigma_Y} $$
Where \( \sigma_X \) is the standard deviation of \( X \) and \( \sigma_Y \) is the standard deviation of \( Y \).
Since we already know the covariance between the variables is \( \text{Cov}(X, Y) = 4.0 \)
$$ r = \frac{4}{\sigma_X \cdot \sigma_Y} $$
First, I calculate the standard deviation \( \sigma_X \):
$$ \sigma_X = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(X_i - \bar{X})^2} $$
$$ \sigma_X = \sqrt{\frac{(1 - 3)^2 + (2 - 3)^2 + (3 - 3)^2 + (4 - 3)^2 + (5 - 3)^2}{5}} $$
$$ \sigma_X = \sqrt{\frac{4 + 1 + 0 + 1 + 4}{5}} = \sqrt{2} \approx 1.414 $$
Next, I calculate the standard deviation \( \sigma_Y \):
$$ \sigma_Y = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(Y_i - \bar{Y})^2} $$
$$ \sigma_Y = \sqrt{\frac{((2 - 6)^2 + (4 - 6)^2 + (6 - 6)^2 + (8 - 6)^2 + (10 - 6)^2}{5}} $$
$$ \sigma_Y = \sqrt{\frac{16 + 4 + 0 + 4 + 16}{5}} = \sqrt{8} \approx 2.828 $$
Now that I have both standard deviations, \( \sigma_X \) and \( \sigma_Y \), I can calculate the Pearson correlation coefficient \( r \):
$$ r = \frac{4.0}{\sigma_X \cdot \sigma_Y} $$
$$ r = \frac{4.0}{1.414 \cdot 2.828} \approx 1.0 $$
In this case, the Pearson coefficient is approximately \( r = 1.0 \), confirming that \( X \) and \( Y \) have a perfect positive correlation.
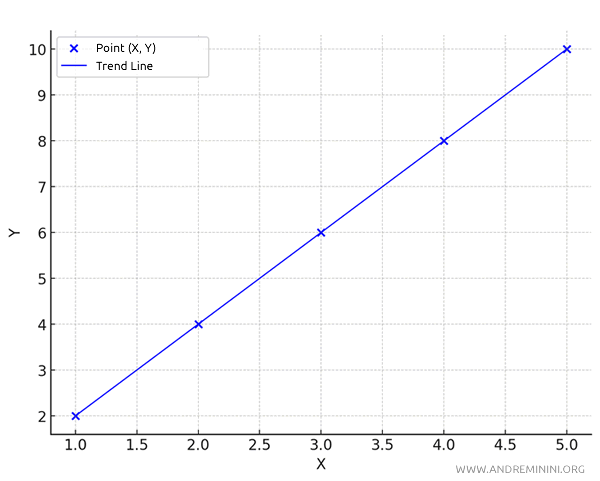
As \( X \) increases, \( Y \) increases as well, and vice versa.
The Difference Between Correlation and Causation
Correlation and causation are two different concepts.
- Correlation: It describes a relationship between two variables, meaning that when one changes, the other tends to change as well—either similarly or oppositely. However, correlation alone does not imply that one variable directly affects the other.
- Causation: This means a cause-and-effect relationship, where one variable (the cause) leads to a change in the other (the effect). To prove causation, you need to demonstrate not only that the variables are correlated but also that one is the direct cause of the other, excluding other potential explanations.
So, even if two variables are correlated, it doesn’t automatically mean one causes the other; there could be external factors or coincidences involved.
In simple terms, correlation means observing that two things occur together. Causation means understanding why they happen.
Example
A study shows that on days when more ice creams are sold, there’s also an increase in the number of people drowning in pools.
Could I conclude that eating ice cream causes drownings? Certainly not. There’s actually a third variable at play: hot weather. When it’s hot, people eat more ice cream and visit the pool more often.
So, the heat is the real cause of both, but ice cream (A) and drownings (B) are merely correlated. There’s no direct cause-and-effect link between them. There’s correlation, but not causation.
The key takeaway: correlation only indicates that two things happen together. Causation, on the other hand, shows that one thing directly influences the other.
Example 2
Looking outside, I notice people carrying umbrellas and wet roads.
These two events often occur together, but it’s not the umbrella causing the wet roads, nor the wet roads causing people to carry umbrellas. Instead, they’re both effects of the same cause: rain.
The rain is the actual cause that leads both to people carrying umbrellas and to wet roads.
Therefore, there is a causal relationship between rain and these two events. However, between people carrying umbrellas and wet roads, there’s only correlation.
And so forth.
