Geometric Mean

The geometric mean is the nth root of the product of n terms. $$ \mu_g = \sqrt[n]{x_1 \cdot x_2 \cdot x_3 \cdot x_4 \cdot ... \cdot x_n } = \sqrt[n]{ \prod_{i=1}^n x_i} $$

What is it used for?

The geometric mean is a measure of central tendency, similar to the arithmetic mean.

However, it doesn't produce the same result as the arithmetic mean.

When to use the geometric mean. The geometric mean is valuable because of its unique characteristics. It is particularly useful for calculating the average of ratios, such as between two series X_i/Y_i. It also applies to calculating the average of growth rates and quantities that are multiplied together. Unlike the arithmetic mean, the geometric mean is more sensitive to very small values. However, it can't be used if any value is zero or negative.

Unlike the arithmetic mean, the geometric mean accounts for the cumulative effect of rates of change.

This makes it especially suited for calculating average growth rates over time, like inflation, population growth, or financial returns.

In such cases, the geometric mean provides a more accurate measure of overall change over time.

A Practical Example

Consider the following data set with n=5 terms:

$$ X = \{ 1 , 2, 3 , 4 , 5 \} $$

The geometric mean of this set is:

$$ \mu_g = \sqrt[5]{ 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 } $$

$$ \mu_g = \sqrt[5]{ 120 } $$

$$ \mu_g = 2.6 $$

The geometric mean of the set X is approximately 2.6.

Notice that the geometric mean differs from the arithmetic mean. In this case, the arithmetic mean of the set X is 3.

$$ \mu = \frac{1+2+3+4+5}{5} = \frac{15}{5} = 3 $$

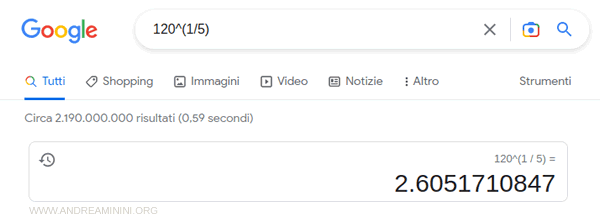
Note. To calculate the nth root on a computer, you can use the invariance property of radicals by raising the radicand to the reciprocal of the root’s index: $$ \mu_g = \sqrt[5]{ 120 } = 120^{1/5} = 2.6 $$ For example, on Google, you can calculate this by typing 120^{1/5} into the search bar and pressing enter.

 

Example 2

Let’s look at a practical example of how the geometric mean is used for growth rates.

I want to calculate the average return on an investment over several years.

Suppose I invested some money, and the annual returns over three years were as follows:

• Year 1: +20%
• Year 2: -10%
• Year 3: +15%

To determine the average annual growth rate, we’ll use the geometric mean.

First, we need to convert the percentage returns into growth factors:

• Year 1: \( 1 + 0.20 = 1.20 \)
• Year 2: \( 1 - 0.10 = 0.90 \)
• Year 3: \( 1 + 0.15 = 1.15 \)

Next, we multiply the growth factors together:

$$ \text{Product} = 1.20 \times 0.90 \times 1.15 = 1.242 $$

The geometric mean is the nth root (where n is the number of periods) of the product of these growth factors:

$$ \text{Geometric Mean} = \sqrt[3]{1.242} \approx 1.075 $$

Finally, to convert the geometric mean into an annual percentage growth rate, we subtract 1 and multiply by 100:

$$ \text{Average Annual Growth Rate} = (1.075 - 1) \times 100\% = 7.5\% $$

So, based on the geometric mean, the average annual growth rate of the investment is 7.5%.

Why use the geometric mean? This method accounts for the cumulative effect of varying rates of return, giving a more accurate picture of how the investment grew over time. If we had used the arithmetic mean, we would have calculated an average return of 8.33%: $$ \text{Arithmetic Mean} = \frac{(+20\% - 10\% + 15\%)}{3} = \frac{25\%}{3} \approx 8.33\% $$ The arithmetic mean does not consider compounding and can overestimate the actual return. By using the geometric mean, we get a more accurate measure of the average annual growth rate when returns are applied sequentially over time. The geometric mean is especially useful when values are interdependent, such as with investment returns, where the return in one year affects the base for the following year’s return.

Difference Between Geometric and Arithmetic Means

The geometric mean is much more sensitive to small values than the arithmetic mean.

Also, if even one term in a data set is zero, the geometric mean will be zero, whereas this isn’t the case with the arithmetic mean.

Example

Consider this set of values:

$$ X = \{ 100, 200, 300, 400, 0.1 \} $$

The arithmetic mean of X is 200.02:

$$ \mu = \frac{100+200+300+400+0.1}{5} = \frac{1000.1}{5} = 200.02 $$

The geometric mean of X is 47.42:

$$ \mu_g = \sqrt[5]{ 100 \cdot 200 \cdot 300 \cdot 400 \cdot 0.1 } = \sqrt[5]{240000000 } = 47.42 $$

The difference between the two averages is quite large.

Example 2

Let’s say the price of a product was €50 at the start of 2019.

In 2019 and 2020, the price increased by 1% each year. In 2021, the price surged by 90%, reaching €96.91 in 2022.

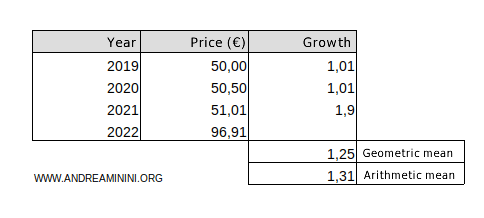
The geometric mean of the growth rates over the three years is 25%:

$$ \mu_g = \sqrt[3]{1,01 \cdot 1,01 \cdot 1,9} = \sqrt[3]{ 1.93819 } = 1.25 $$

The arithmetic mean of the growth rates is 31%:

$$ \mu = \frac{1,01 + 1,01 + 1,9}{3} = \frac{3,92}{3} = 1.31 $$

Which is more accurate?

To find out, let’s run a simulation.

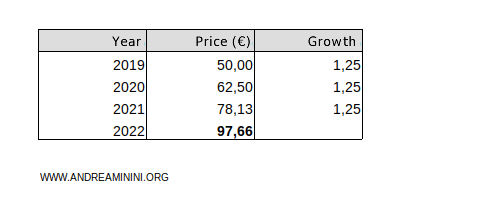
Using the 25% average annual rate (1.25) from the geometric mean, the final price would be 50·1.25³=€97.6.

Using the 31% average annual rate (1.31) from the arithmetic mean, the final price would be 50·1.31³=€112.4.

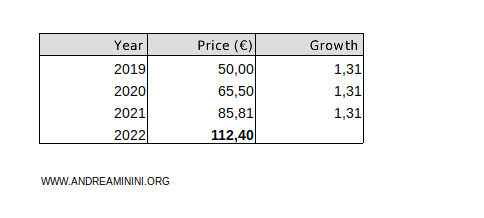
The price closest to the actual price of €96.91 in 2022 is the one calculated using the geometric mean (€97.6).

Therefore, in this case, the geometric mean is more accurate.

Key Takeaways

Here are some important points about the geometric mean:

• The geometric mean of a ratio between two series X_i/Y_i is equal to the ratio of the geometric means of the two series: $$ \mu_g ( \frac{X_i}{Y_i} ) = \frac{\mu_g (X)}{\mu_g(Y)} $$ This makes it useful for calculating the average of ratios, which is not a property of the arithmetic mean.
• The geometric mean cannot be calculated if any term in the data set is zero, because the product of the terms will be zero.
• The geometric mean also cannot be calculated with negative values, as taking the even root of a negative number doesn't result in a real solution.
• The geometric mean is much more sensitive to small values (as long as they’re not zero) because the product decreases significantly when one of the terms is very small. This doesn’t happen with the arithmetic mean.
• The geometric mean equals the arithmetic mean when all terms in a data set are the same.
• You can also calculate the geometric mean using a formula involving exponents and natural logarithms, yielding the same result: $$ \mu_g = e^{ \ \frac{1}{n} \cdot \sum_{i=1}^n \ln x_i \ } $$

  Example. Consider this data set of n=5 terms: $$ X = \{ 1 , 2 , 3 , 4 , 5 \} $$ The average of the natural logarithms of the terms is 0.96: $$ \frac{\ln(1) + \ln(2) + \ln(3)+ \ln(4) + \ln(5)}{5} = \frac{4.79}{5} = 0.96 $$ The exponential of 0.96 is approximately 2.6: $$ e^{0.96} = 2.6 $$ This matches the result from the previous example.

• Weighted Geometric Mean
  The weighted geometric mean is a variation where each term is assigned a weight (w_i): $$ \mu = \sqrt[ \sum{w_i} \ ]{\prod_{i=1}^n x_i^{w_i} } $$

And so on.