Median

The median is the middle value that splits an ordered distribution into two equal-sized groups.

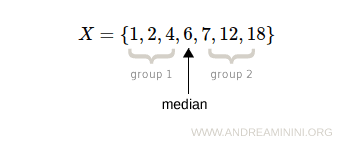
The first group contains all values less than or equal to the median.

The second group contains all values greater than or equal to the median.

How to find the median

First, sort the distribution in ascending order.

Then, determine the median's position, depending on whether the distribution has an odd or even number of terms:

• If the distribution has an odd number of terms (n), the median is the value at the central position (c): $$ c = \frac{n+1}{2} $$

  In this case, the median is simply the value of the term x_c in the ordered distribution: $$ \mu = x_c $$

• If the distribution has an even number of terms (n), the median is the average of the two central values at positions c₁ and c₂: $$ c_1 = \frac{n}{2} $$ $$ c_2 = \frac{n}{2} + 1 $$

  In this scenario, the median is the mean of the terms x_c1 and x_c2 in the ordered distribution: $$ \mu = \frac{x_{c1} + x_{c2} }{2} $$

A practical example

Consider the distribution:

$$ X = \{ 4,1,7,2,6,18,12 \} $$

Sort it in ascending order:

$$ X = \{ 1,2,4,6,7,12,18 \} $$

Assign each term an increasing index, starting from 1:

$$ x_1 = 1 \\ x_2=2 \\ x_3 = 4 \\ x_4 = 6 \\ x_5=7 \\ x_6=12 \\ x_7=18 $$

This distribution has n=7 elements.

Since n is odd, we use the formula to find the median's position:

$$ c = \frac{n+1}{2} = \frac{7+1}{2} = \frac{8}{2} = 4 $$

The median is the term at position c=4.

Thus, the median is the value x₄ = 6.

$$ \mu_e = x_c = x_4 = 6 $$

This median divides the distribution into two groups of three elements each.

Example 2

Consider the distribution:

$$ X = \{ 3,8,12,2,6,7,3,18 \} $$

Sort it in ascending order:

$$ X = \{ 2,3,3,6,7,8,12,18 \} $$

Assign each term an increasing index:

$$ x_1 = 2 \\ x_2=3 \\ x_3 = 3 \\ x_4 = 6 \\ x_5=7 \\ x_6=8 \\ x_7=12 \\ x_8=18 $$

This distribution has n=8 elements.

Since n is even, find the two central positions c₁ and c₂:

$$ c_1 = \frac{n}{2} = \frac{8}{2} = 4 $$

$$ c_2 = \frac{n}{2} + 1 = \frac{8}{2} + 1 = 4 + 1 = 5 $$

The values at these positions are x₄ = 6 and x₅ = 7.

$$ x_{c1} = x_4 = 6 $$

$$ x_{c2} = x_5 = 7 $$

The median is the average of these two values:

$$ \mu_e = \frac{x_{c1} + x_{c2}}{2} = \frac{6 + 7}{2} = \frac{13}{2} = 6.5 $$

Therefore, the median is 6.5.

$$ \mu_e = 6.5 $$

Note: When the distribution has an even number of elements, the median may not necessarily be one of the values in the distribution. For instance, here the median value 6.5 is not part of the original distribution X = {4,1,7,2,6,18,12}.

The median in a frequency distribution

To find the median in a frequency distribution:

1. Calculate the cumulative absolute frequency by adding each frequency to the sum of all previous frequencies.
2. Identify the median's position (c) in the cumulative frequency:

   If the cumulative frequency is even, the median position is $$ c = \frac{ \sum_{k=1}^n f_k}{2} $$. If it's odd, the median position is $$ c = \frac{ 1 + \sum_{k=1}^n f_k}{2} $$.

3. Find the cumulative frequency that includes the median's position (c).
4. The class associated with that cumulative frequency is the median class.

Example

Consider this frequency distribution:

Add a column for the cumulative absolute frequencies:

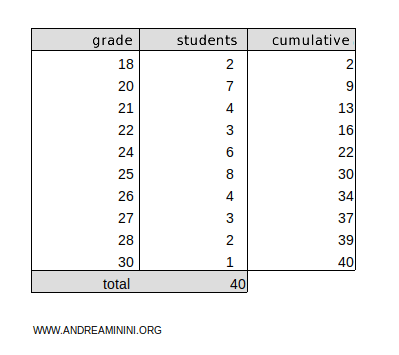
The total cumulative frequency is 40.

Since it's even, use the formula to find the median's position:

$$ c = \frac{ \sum_{k=1}^n f_k}{2} = \frac{40}{2} = 20 $$

The median position is c = 20.

Next, check which cumulative frequency contains the median's position c = 20.

Here, the median position c = 20 falls within the cumulative frequency range 16-22, which corresponds to the class 24.

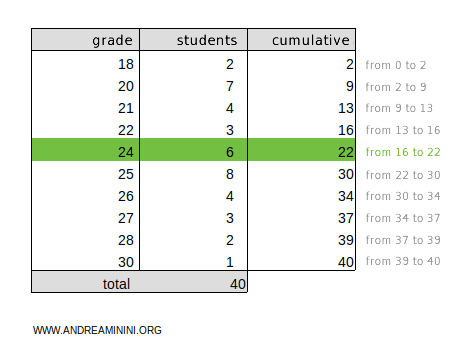
Thus, the median class for this distribution is 24.

$$ \mu_e = 24 $$

Example 2

Consider this frequency distribution divided into classes:

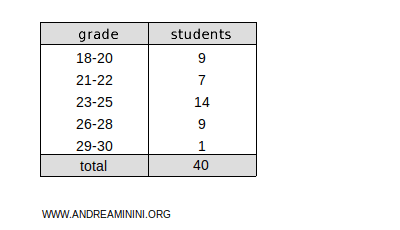
Each class represents a range of values.

Add a column for the cumulative absolute frequencies:

Again, the total cumulative frequency (40) is an even number.

So, use the formula to find the median's position:

$$ c = \frac{ \sum_{k=1}^n f_k}{2} = \frac{40}{2} = 20 $$

The median position is c = 20.

This position falls within the 23-25 class.

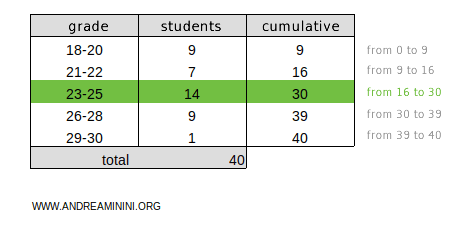
Therefore, the median is the class 23-25.

To calculate the precise median value, use linear interpolation within the 23-25 class:

$$ \mu_e = x_{inf} + (x_{sup} - x_{inf}) \cdot \frac{ c - n_{prec} }{n_{classe}} $$

Here's what each term represents:

• x_inf = 23 and x_sup = 25 are the boundaries of the 23-25 class.
• c = 20 is the median's position.
• n_classe = 14 is the frequency of the 23-25 class.
• n_prec = 16 is the cumulative frequency of the classes before the 23-25 class.

Substitute the values and perform the calculations:

$$ \mu_e = 23 + (25 - 23) \cdot \frac{ 20 - 16 }{14} $$

$$ \mu_e = 23 + 2 \cdot \frac{ 4 }{14} $$

$$ \mu_e = 23 + \frac{4}{7} $$

$$ \mu_e = 23 + 0.57 $$

$$ \mu_e = 23.57 $$

The median value is 23.57.

Note: You can arrive at the same result by setting up a proportion between the class values and the cumulative frequencies: $$ (25-23):(x-23) = (30-16):(c-16) $$ where the median position is c = 20: $$ (25-23):(x-23) = (30-16):(20-16) $$ $$ 2:x-23 = 14:4 $$ Rewrite the proportion as a fraction: $$ \frac{2}{x-23} = \frac{14}{4} $$ Solve for x: $$ \frac{2}{\frac{14}{4} } = x-23 $$ $$ 2 \cdot \frac{4}{14} + 23 = x $$ $$ x = \frac{4}{7} + 23 = 23.57 $$ The final result is the same.

Key Points

Here are some important points about the median:

• The median is not affected by extremely high or low values or outliers in the distribution, unlike the arithmetic mean.

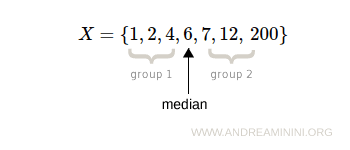
  Example: The median of the distribution X = {4,1,7,2,6,18,12} is μ_e = 6.
  
  If you replace the last term (12) with 200, the median remains μ_e = 6.
  

• Sum of absolute differences
  The sum of the absolute differences between the values in a set and the median is always smaller than that obtained with any other value.

  Example: For this set of data: $$ \{ 1, 2, 4, 6, 7, 12, 18 \} $$ Since the set has an odd number of elements (\(7\)), the median is the central value, which is \(6\). Calculate the sum of the absolute differences from \(6\): $$ |1 - 6| + |2 - 6| + |4 - 6| + |6 - 6| + |7 - 6| + |12 - 6| + |18 - 6| $$ $$ 5 + 4 + 2 + 0 + 1 + 6 + 12 = 30 $$ So, the sum of absolute differences from the median (\(6\)) is \(30\). Now, let's find the sum of absolute differences from another value, say \(7\): $$ |1 - 7| + |2 - 7| + |4 - 7| + |6 - 7| + |7 - 7| + |12 - 7| + |18 - 7| $$ $$ 6 + 5 + 3 + 1 + 0 + 5 + 11 = 31 $$ The sum of absolute differences from \(7\) is \(31\), which is greater than that obtained with the median (\(30\)). Similarly, for any other value different from the median, the sum of absolute differences will always be greater than or equal to that obtained with the median.

And so forth.