Weighted Average
An average is referred to as a weighted average when the terms are multiplied by a weight. It is calculated by dividing the sum of the products of each number and its corresponding weight by the sum of the weights. $$ \mu = \frac{ x_1 p_1 + x_2 p_2 + ... + x_n p_n }{ p_1 + p_2 + ... + p_n } $$ Here, x1, x2, ..., xn represent the values, and p1, p2, ..., pn are their respective weights.
A weighted average differs from a simple average, where all terms contribute equally to the result, without any weighting.
There are several types of weighted averages:
When the weights p1, p2, ... , pn represent frequencies, the weighted average simplifies to a regular average, just expressed differently.
However, when the weights reflect subjective importance or other variables, the weighted average allows you to account for those differences.
For example, in a university exam that consists of both a written and an oral component, you might use a weighted average to place more emphasis on the written score rather than simply calculating a regular arithmetic mean.
A Practical Example
Let’s walk through a practical example of a weighted arithmetic average.
Consider this table showing the results of an exam session.
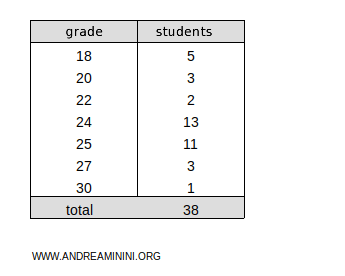
The same scores are counted multiple times in the calculation because several students achieved the same grade.
Note: For example, five students received a score of 18, three students scored 20, two got 22, and so on.
In this case, the grades are the terms, and the number of students (absolute frequencies) are the weights.
To calculate the weighted arithmetic average, we use this formula:
$$ \mu = \frac{\sum_{i=1}^k x_i \cdot p_i }{ \sum_{i=1}^k p_i } $$
Where x represents the terms (grades), and p represents the weights or frequencies (number of students).
The weighted arithmetic average is the sum of the products of each grade and its frequency, divided by the total number of students.
$$ \mu = \frac{18 \cdot 5 + 20 \cdot 3 + 22 \cdot 2 + 24 \cdot 13 + 25 \cdot 11 + 27 \cdot 3 + 30 \cdot 1}{5+3+2+13+11+3+1} $$
$$ \mu = \frac{90 + 60 + 44 + 312 + 275 + 81 + 30}{38} $$
$$ \mu = \frac{892}{38} $$
$$ \mu = 23.47 $$
Therefore, the weighted arithmetic average for this distribution is μ = 23.47.
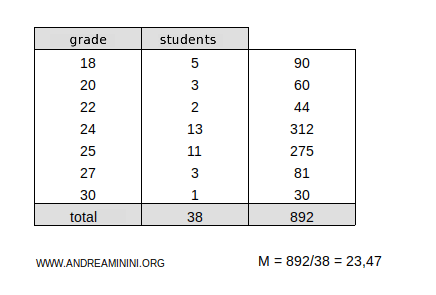
In this example, the weights represent the frequencies.
Thus, the result is the same as if we calculated the arithmetic mean of all the students' grades individually.
Example 2
Here’s another example of a weighted average calculation using a table that shows a student’s scores for both a written and an oral exam.
In this case, the written exam score is weighted twice as heavily as the oral exam score.
| Exam | Score | Weight |
|---|---|---|
| Written | 28 | 2 |
| Oral | 24 | 1 |
To calculate the weighted average, we use the following formula:
$$ \text{Weighted Average} = \frac{\sum (score \times weight)}{\sum weights} $$
In this case, the written score is 28 with a weight of 2, and the oral score is 24 with a weight of 1.
$$ \text{Weighted Average} = \frac{(28 \times 2) + (24 \times 1)}{2 + 1} = \frac{56 + 24}{3} = \frac{80}{3} \approx 26.67 $$
So, the weighted average for this exam, considering the weights, is approximately 26.67.
In this case, the weights are subjective, based on the emphasis you want to place on each part of the exam. Here, the written exam is given more importance.
Note: If we had calculated the arithmetic mean, the final result would have been 26. The arithmetic mean is a weighted average where each value has equal weight, such as a unit weight for each value.
And so on...
