Solved exercises on rings

Some worked exercises on rings

Exercise 1

We aim to determine whether the set of integers Z₅ = {0, 1, 2, 3, 4}, equipped with addition and multiplication modulo 5, forms a ring:

$$ (Z_5 ,+_5, \cdot_5) $$

Since Z₅ is a finite set, we can explicitly construct its addition table:

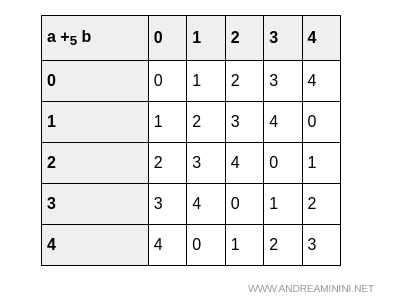
And similarly, the multiplication table:

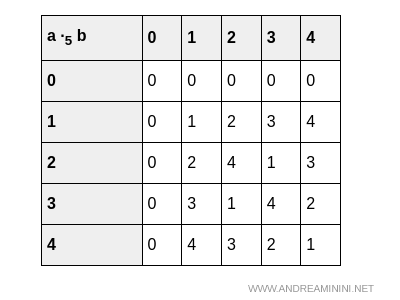
Both operations are closed on Z₅, fulfilling the first requirement for a ring.

We now proceed to verify whether the remaining ring axioms are satisfied.

The First Operation: Addition (+₅)

Modulo 5 addition on Z₅ is commutative:

$$ a +_5 b = b +_5 a \quad \forall \ a, b \in Z_5 $$

It is also associative:

$$ (a +_5 b) +_5 c = a +_5 (b +_5 c) \quad \forall \ a, b, c \in Z_5 $$

The additive identity is 0:

$$ a +_5 0 = 0 +_5 a = a \quad \forall \ a \in Z_5 $$

Every element in Z₅ has an additive inverse. For example:

0 + 0 = 0, 1 + 4 = 0, 2 + 3 = 0, and so on.

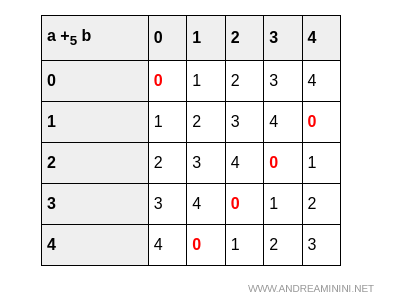
Therefore, all the axioms for the additive structure of a ring are satisfied.

Note: The structure (Z₅, +) forms a group since Z₅ is non-empty, addition modulo 5 is closed and associative, has an identity element (0), and each element has an inverse. Furthermore, because addition is commutative, (Z₅, +) is an abelian group, satisfying the first fundamental requirement for a ring.

The Second Operation: Multiplication (·₅)

Modulo 5 multiplication on Z₅ is associative:

$$ (a \cdot_5 b) \cdot_5 c = a \cdot_5 (b \cdot_5 c) \quad \forall \ a, b, c \in Z_5 $$

It also distributes over addition, both from the left and from the right:

$$ (a +_5 b) \cdot_5 c = a \cdot_5 c +_5 b \cdot_5 c \quad \forall \ a, b, c \in Z_5 $$

$$ a \cdot_5 (b +_5 c) = a \cdot_5 b +_5 a \cdot_5 c \quad \forall \ a, b, c \in Z_5 $$

Thus, all the ring axioms pertaining to multiplication are satisfied.

Conclusion

Since both operations satisfy the required axioms, we conclude that:

The algebraic structure (Z₅, +, ·) is a ring.

Exercise 2

We wish to determine whether the function \( f(x) = |x| \) defines a ring homomorphism between the rings \( (\mathbb{Z}, +, \cdot) \) and \( (\mathbb{Z}', +, \cdot) \), where \( \mathbb{Z} = \mathbb{Z}' \).

We begin by checking whether \( f \) preserves multiplication, as required for a ring homomorphism:

$$ f(a \cdot b) = f(a) \cdot f(b) $$

$$ |a \cdot b| = |a| \cdot |b| $$

This equality always holds, since the absolute value of a product equals the product of the absolute values.

Note: On the left-hand side, the absolute value of the product is always non-negative. On the right-hand side, the product of two non-negative numbers (i.e., the absolute values) is also non-negative. Therefore, the two expressions agree.

Next, we examine whether \( f \) preserves addition:

$$ f(a + b) = f(a) + f(b) $$

$$ |a + b| = |a| + |b| $$

This identity does not hold in general - specifically, it fails whenever \( a \) and \( b \) have opposite signs.

For instance, consider \( a = 2 \) and \( b = -3 \):

$$ |2 + (-3)| \ne |2| + |-3| $$

$$ |-1| \ne 2 + 3 $$

$$ 1 \ne 5 $$

Since the function fails to preserve addition, it does not satisfy the defining properties of a ring homomorphism.

We conclude that the function \( f(x) = |x| \) is not a ring homomorphism from \( (\mathbb{Z}, +, \cdot) \) to \( (\mathbb{Z}', +, \cdot) \).

Exercise 3

Is the set of integers Z₆ = {0, 1, 2, 3, 4, 5} a ring, with addition defined as modulo 6 addition and multiplication defined as modulo 6 multiplication?

$$ (Z_6 ,+_6, \cdot_6) $$

Since Z₆ is a finite set, we begin by constructing the addition table:

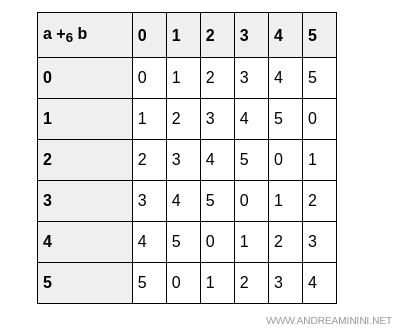
And now the multiplication table:

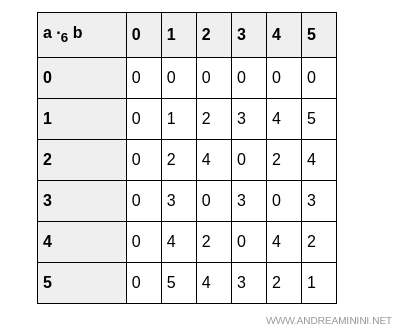
Both addition and multiplication are binary operations that are closed on Z₆, so the first requirement for a ring is satisfied.

Let’s now verify whether the remaining ring axioms hold.

The First Operation (+₆)

Addition modulo 6 is commutative on Z₆:

$$ a +_6 b = b +_6 a \quad \forall \ a, b \in Z_6 $$

It is also associative:

$$ (a +_6 b) +_6 c = a +_6 (b +_6 c) \quad \forall \ a, b, c \in Z_5 $$

The additive identity is 0:

$$ a +_5 0 = 0 +_5 a = a \quad \forall \ a \in Z_5 $$

Moreover, every element in Z₆ has an additive inverse.

For example: 0 + 0 = 0, 1 + 5 = 0, 2 + 4 = 0, 3 + 3 = 0, etc.

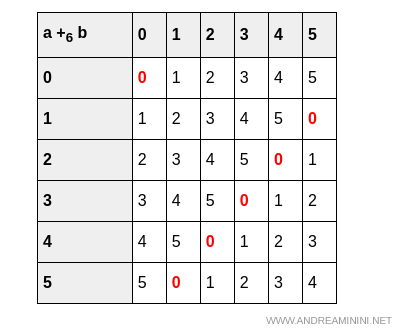
Therefore, the addition operation satisfies all the axioms required of a ring.

Note. The structure (Z₆, +) forms a group, as Z₆ is non-empty, addition modulo 6 is closed and associative, there exists an identity element (0), and each element has an inverse. Since addition is also commutative, (Z₆, +) is in fact an abelian group.

The Second Operation (·₆)

Multiplication modulo 6 is associative over Z₆:

$$ (a \cdot_6 b) \cdot_6 c = a \cdot_6 (b \cdot_6 c) \quad \forall \ a, b, c \in Z_6 $$

It also satisfies the distributive laws with respect to addition:

$$ (a +_6 b) \cdot_6 c = a \cdot_6 c +_6 b \cdot_6 c \quad \forall \ a, b, c \in Z_6 $$

$$ a \cdot_6 (b +_6 c) = a \cdot_6 b +_6 a \cdot_6 c \quad \forall \ a, b, c \in Z_6 $$

Hence, the multiplication operation meets all the ring requirements.

Conclusion

To conclude, both binary operations satisfy the axioms of a ring.

Therefore, we can affirm that the algebraic structure (Z₆, +, ·) is a ring.

Exercise 4

We want to determine whether the function f(x) = 3x defines a ring homomorphism between the rings (Z₆, +, *) and (Z₆', +, *), where both addition and multiplication are taken modulo 6.

As a first step, let’s construct the addition table modulo 6.

Now let’s build the multiplication table modulo 6.

We now verify whether the function satisfies the first condition for being a ring homomorphism:

$$ f(a + b) = f(a) + f(b) $$

Since f(x) = 3x, we have:

$$ 3 \cdot (a + b) = 3a + 3b $$

This identity holds true modulo 6, so the function preserves addition.

Next, we test whether f(x) also preserves multiplication:

$$ f(a \cdot b) = f(a) \cdot f(b) $$

Substituting again:

$$ 3 \cdot (a \cdot b) = 3a \cdot 3b $$

By associativity and modular arithmetic, the equality is verified.

Therefore, the function f(x) = 3x is a ring homomorphism from (Z₆, +, *) to itself.

Verification

Since we are working with a small, finite ring, it’s useful to explicitly display the tables for the homomorphism to confirm the result.

For addition, both 3(a + b) and 3a + 3b yield the same table:

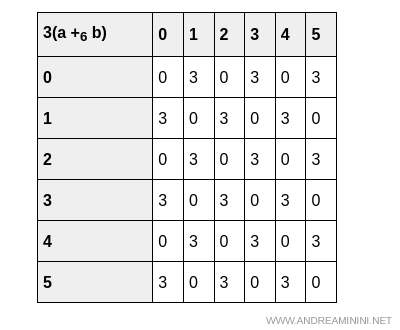
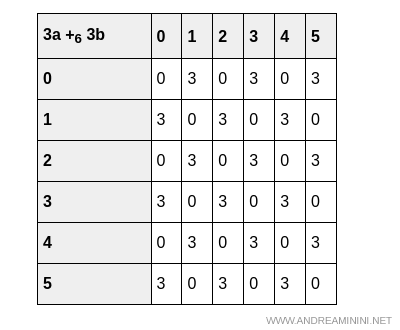
Even in the case of multiplication, the two tables $3(a \cdot b)$ and $(3a) \cdot (3b)$  yield the same result.

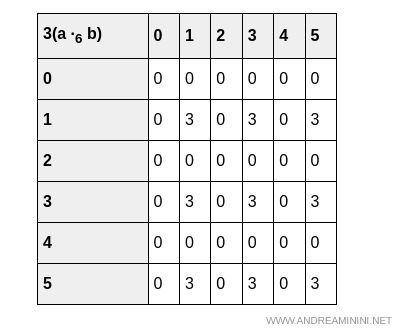
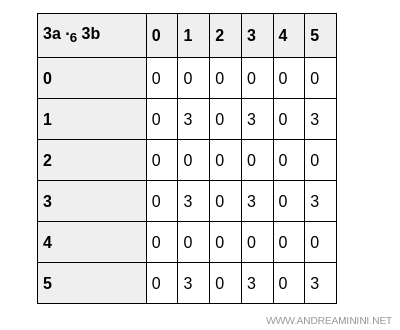
This thorough verification fully confirms the previous solution.

The mapping $f(x) = 3x$ defines a ring homomorphism between the rings $(\mathbb{Z}_6, +, \cdot)$ and $(\mathbb{Z}_6, +, \cdot)$.