Tertiles

What are tertiles?

Tertiles are two quantiles that divide a statistical distribution into three equal parts.

Each part contains an equal number of elements.

There are two tertiles:

• The first tertile (T₁) separates the first 1/3 (33.33%) of the distribution from the remaining 2/3 (66.67%).
• The second tertile (T₂) separates the first 2/3 (66.67%) of the distribution from the remaining 1/3 (33.33%).

Example. In this dataset, the first tertile T₁=5.5 and the second tertile T₂=8.5 divide the distribution into three equal parts: $$X = \{ \underbrace{3,4,5},\color{red}{T_1}, \underbrace{6,7,8}, \color{red}{T_2}, \underbrace{9,10,11} \}$$

How to calculate tertiles

To calculate tertiles, we distinguish between ordered sequences and frequency distributions.

Ordered sequences

For an ordered sequence (a sorted list of values), the steps to calculate tertiles are:

1. Sort the data in ascending order.
2. Multiply the total number of elements (n) by p=1/3 for T₁ and p=2/3 for T₂: $$k = n \cdot p$$
3. Find the position of the tertile:
   • If k is an integer, the tertile is the average of the k-th and (k+1)-th elements.
   • If k is not an integer, round up to the next whole number to find the tertile.

Frequency distributions

For frequency distributions, the process is slightly different:

• Calculate the cumulative frequencies for each class.
• Divide the total cumulative frequency by 1/3 and 2/3 to find the positions of T₁ and T₂ within the cumulative frequency distribution.
• Locate the class intervals corresponding to these positions. The tertiles fall within these intervals.

Note. Various methods exist for calculating tertiles. Some use linear interpolation to estimate the tertile within a class, while others approximate the tertile based on the class mean.

Practical example

Example 1

Consider a dataset with n=9 elements:

$$X = \{ 9,6,11,8,4,7,10,3,5 \}$$

First, sort the data in ascending order:

$$X = \{ 3,4,5,6,7,8,9,10,11 \}$$

To calculate the first tertile (T₁), multiply the number of elements by 1/3:

$$k = n \cdot \frac{1}{3} = 9 \cdot \frac{1}{3} = 3$$

The result is an integer, so we calculate the average of the third (k=3) and fourth (k+1=4) elements:

$$X = \{ 3,4,\underbrace{5,6},7,8,9,10,11 \}$$

The third element is 5, and the fourth is 6:

$$T_1 = \frac{5+6}{2} = 5.5$$

Thus, the first tertile of the distribution is T₁=5.5.

$$T_1 = 5.5$$

To calculate the second tertile (T₂), multiply the number of elements by 2/3:

$$k = n \cdot \frac{2}{3} = 9 \cdot \frac{2}{3} = 6$$

Again, the result is an integer, so we calculate the average of the sixth (k=6) and seventh (k+1=7) elements:

$$X = \{ 3,4,5,6,7,\underbrace{8,9},10,11 \}$$

The sixth element is 8, and the seventh is 9:

$$T_2 = \frac{8+9}{2} = 8.5$$

Thus, the second tertile is T₂=8.5.

$$T_2 = 8.5$$

In summary, the two tertiles T₁ = 5.5 and T₂ = 8.5 divide the distribution into three equal parts:

$$X = \{ \underbrace{3,4,5},\color{red}{T_1}, \underbrace{6,7,8}, \color{red}{T_2}, \underbrace{9,10,11} \}$$

Note. In this case, the tertiles do not correspond to elements in the original dataset.

Example 2

Now, consider the same dataset with one element removed. The new dataset has n=8 elements:

$$X = \{ 9,6,8,4,7,10,3,5 \}$$

After sorting the data in ascending order:

$$X = \{ 3,4,5,6,7,8,9,10 \}$$

To calculate the first tertile (T₁), multiply the number of elements by 1/3:

$$k = n \cdot \frac{1}{3} = 8 \cdot \frac{1}{3} = 2.66$$

Since the result is not an integer, round up to the next whole number: k=3.

$$X = \{ 3,4,\color{red}5,6,7,8,9,10 \}$$

The third element is 5.

Thus, the first tertile is T₁=5.

$$T_1 = 5$$

To calculate the second tertile (T₂), multiply the number of elements by 2/3:

$$k = n \cdot \frac{2}{3} = 8 \cdot \frac{2}{3} = 5.33$$

Again, round up to the next whole number: k=6.

$$X = \{ 3,4,5,6,7,\color{red}8,9,10 \}$$

The sixth element is 8.

Thus, the second tertile is T₂=8.

$$T_2 = 8$$

In this case, the two tertiles T₁ = 5 and T₂ = 8 divide the distribution into three equal parts:

$$X = \{ \underbrace{3,4},\color{red}{5}, \underbrace{6,7}, \color{red}{8}, \underbrace{9,10} \}$$

Note. Here, the tertiles correspond to elements in the dataset.

Example 3

Consider the following frequency distribution:

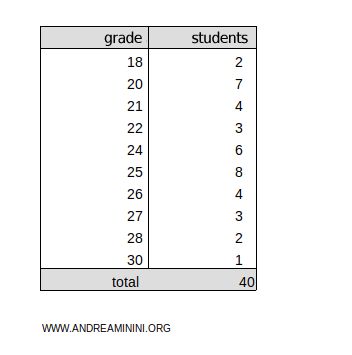
In this example, exam scores are the observed values, and the number of students represents the absolute frequencies.

To find the tertiles, first calculate the cumulative frequencies for each class:

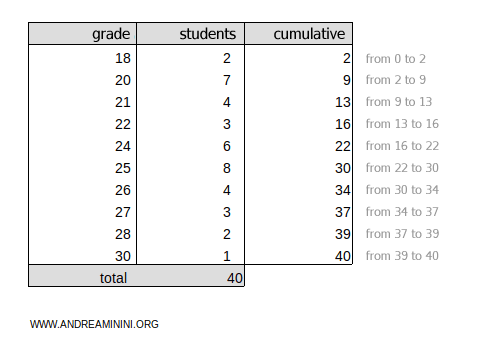
The total cumulative frequency is f_tot=40.

To find the first tertile, multiply the total cumulative frequency f_tot by 1/3:

$$k =f_{tot} \cdot \frac{1}{3} = 40 \cdot \frac{1}{3} = 13.3$$

The result 13.3 falls within the cumulative frequency range of 13-16.

Therefore, the first tertile is within the class T₁=22.

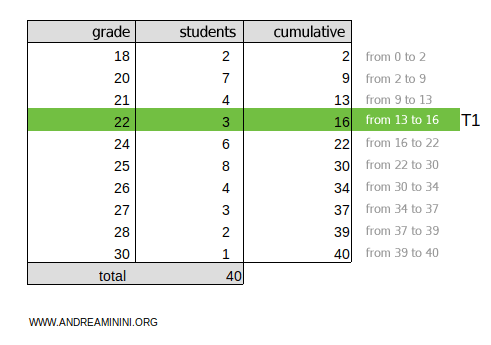
To find the second tertile, multiply the total cumulative frequency f_tot by 2/3:

$$k =f_{tot} \cdot \frac{2}{3} = 40 \cdot \frac{2}{3} = 26.6$$

The result 26.6 falls within the cumulative frequency range of 22-30.

Therefore, the second tertile is within the class T₂=25.

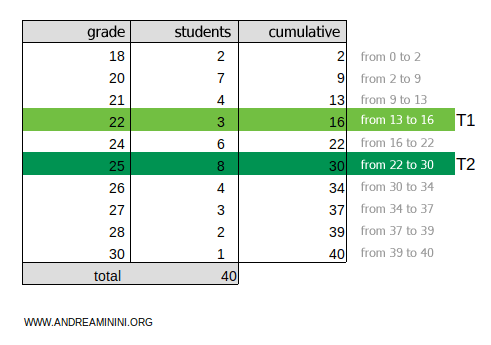
And so on.