Angular Momentum

What determines angular momentum?

Angular momentum depends on:

• the body’s position $ \vec{r} $ relative to the reference point $ O $
• the body’s linear momentum $ \vec{p} = m \vec{v} $
• the orientation of the motion relative to the position vector

For instance, in non-uniform circular motion, a body travels along a circular path with a tangential speed that varies over time.

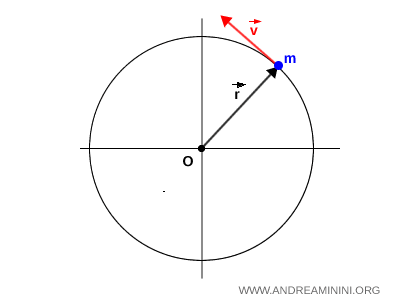
Here, the distance $ r $ between the body and the center of rotation $ O $ is constant. If the body’s mass $ m $ is also fixed, angular momentum is directly proportional to the tangential velocity $ \vec{v} $.

Note. Even a body moving in a straight line can possess angular momentum, provided its path does not pass through the chosen reference point $ O $. In that case, the position vector $\vec{r}$ relative to $ O $ still changes over time.

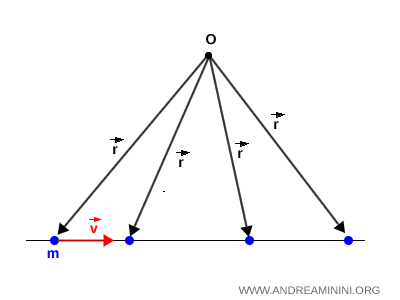
By contrast, if the straight-line motion passes directly through $ O $, the angular momentum remains zero at all distances.

The magnitude of angular momentum depends on the angle $ \theta $ between $ \vec{r} $ and $ \vec{v} $:

$$ L = mrv \cdot \sin \theta $$

This value ranges between two limits:

• When $ \theta = 90^\circ $, angular momentum is maximized at $ L = mrv $, since $ \vec{r} $ and $ \vec{v} $ are perpendicular.
• When $ \theta = 0^\circ $ or $ \theta = 180^\circ $, angular momentum vanishes $ L=0 $, because $ \vec{r} $ and $ \vec{v} $ are parallel.

In general, angular momentum depends on several factors: a body's mass, its perpendicular distance from the axis of rotation, its tangential velocity, and the reference frame used to describe its motion.

Its value can also change when measured relative to a different point $ O $. This means that angular momentum is not an inherent property of the object, but a quantity that only takes shape within a chosen frame of reference.

A Practical Example

Consider an athlete preparing for the hammer throw.

The hammer has a mass $m = 7{,}26\,\text{kg}$ and is attached to a wire of length $r = 1{,}20\,\text{m}$.

As the athlete spins, the hammer traces a horizontal circle around the grip point, which serves as the center of rotation. During this phase, the athlete steadily increases the hammer’s tangential speed.

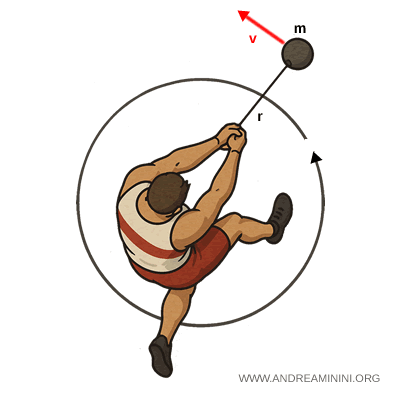
At the instant of release, if the hammer’s tangential speed is $v = 28{,}0\,\text{m/s}$, the angular momentum about the center of rotation is given by:

$$ L = m r v $$

Substituting the values:

$$ L = (7{,}26\,\text{kg}) \cdot (1{,}20\,\text{m}) \cdot (28{,}0\,\text{m/s}) $$

$$ L \approx 243{,}94\,\text{kg·m}^2/\text{s} $$

Thus, at the moment of release the angular momentum is $ L \approx 243{,}94\,\text{kg·m}^2/\text{s} $.

This result depends on three key factors:

• The hammer’s mass: the heavier it is, the greater $L$.
• The radius: the longer the lever arm, the larger $L$.
• The tangential speed: this is the decisive factor, since it is what the athlete actively controls during the throw.

If, for example, the athlete released the hammer at half the speed, $v = 14{,}0\,\text{m/s}$, the angular momentum would be lower:

$$ L = 7{,}26 \cdot 1{,}20 \cdot 14{,}0 = 121{,}968 \approx 121{,}97\,\text{kg·m}^2/\text{s} $$

This means that less force would be required to stop or alter the rotational motion relative to the pivot.

Note. In the hammer throw, both the mass $ m $ and the radius $ r $ are constant. In such cases, angular momentum is directly proportional to tangential speed $ v $. Put simply: the faster the hammer spins, the harder it is to stop. That said, a more refined analysis must also account for variations in the effective radius due to the athlete’s body movements and arm length, which modify $ r $ and therefore angular momentum as well.

Conservation of Angular Momentum

If no external torques act on a system, its total angular momentum is conserved.

This principle underlies a wide range of physical phenomena.

For instance, it explains why a figure skater spins faster when pulling in their arms, or why satellites and planets follow stable orbits.

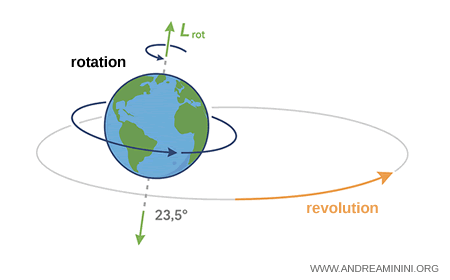
Earth's Angular Momentum

Earth has two distinct forms of angular momentum, each tied to a different type of motion that shapes the way our planet behaves in space.

• Rotational angular momentum
  The first form comes from Earth's rotation on its axis, a full spin completed in about 24 hours. This angular momentum depends on several factors: Earth's mass, its radius, how that mass is distributed, and the angular velocity of rotation $ \omega $. This rotational momentum helps keep Earth's axis stable, which is why the rhythm of day and night remains so regular over long periods of time.

  Note. For a rigid body, the rotational angular momentum is $$ L_{\text{rot}} = I  \omega $$ where $ I $ is the moment of inertia and $ \omega $ is the angular velocity. For an oblate sphere like Earth, a common approximation is $$ I \approx \frac{2}{5} M R^2 $$ and $$ \omega = \frac{2\pi}{T_{\text{rot}}} $$ with $ T_{\text{rot}} \approx 24,\text{h} $.

• Orbital angular momentum
  The second form comes from Earth's revolution around the Sun, a journey completed in roughly 365 days. In this case, angular momentum depends on Earth's mass, its distance from the Sun, and its orbital speed. This quantity plays a key role in keeping Earth's orbit stable over time. For an orbiting body, the orbital angular momentum is $$  L_{\text{orb}} = m v r $$  or, in vector form, $$ \mathbf{L}_{\text{orb}} = \mathbf{r} \times \mathbf{p} $$ where $ m $ is Earth's mass, $ v $ is its orbital velocity, and $ r $ is the average Earth - Sun distance.

  Note. Because orbital motion also satisfies the relation $ v = \omega_{\text{orb}} r $, we can rewrite the orbital angular momentum as $$ L_{\text{orb}} = m, r^2, \omega_{\text{orb}} $$ where $ \omega_{\text{orb}} = \frac{2\pi}{T_{\text{orb}}} $ and $ T_{\text{orb}} \approx 365,\text{giorni} $.

In both cases, the principle of conservation of angular momentum is fundamental. It is this conservation that helps Earth maintain a stable orbit and ensures that its axis continues to point in almost the same direction in space.

And so on.