Difference Between Rounding and Truncation

An approximation by truncation is achieved by cutting off the decimal digits beyond a set point. On the other hand, rounding picks the number closest to the original, increasing the last retained digit if the first omitted digit is 5 or greater.

Approximating a real number \( r \) is common practice in mathematics and sciences to manage numbers with long decimal strings, especially when measurement precision is limited by available tools.

Moreover, some real numbers, like pi \( \pi = 3.1415926... \) or the square root of two \( \sqrt{2}=1.41421... \), are irrational, meaning they have an infinite, non-repeating decimal part.

In these cases, approximation is essential for representing and using such numbers in calculations, while keeping precision within acceptable limits.

Truncation vs. Rounding

Two main ways to approximate a real number are truncation and rounding.

• Truncation
  Truncation reduces a number by cutting off all decimals beyond a specified point without altering any digits. This method is ideal when a conservative, lower estimate than the actual value is needed.

  Example. Truncating \( \pi = 3.1415926... \) to three decimal places gives \( \pi \approx 3.141 \).

• Rounding
  Rounding selects the value that’s closest to the real number \( r \) with the specified number of decimal places. To decide whether to round up or down, check the first omitted decimal place:
  • If the omitted digit is less than 5, the rounded result matches the truncated value.
  • If the omitted digit is 5 or greater, the last kept digit is increased by one.

  Example. Rounding \( \pi = 3.1415926... \) to three decimal places results in \( \pi \approx 3.142 \) since the first omitted digit is 5 (i.e.,  \( \pi = 3.141\color{red}{5}926... \)), rounding up to \( 3.142 \).
  

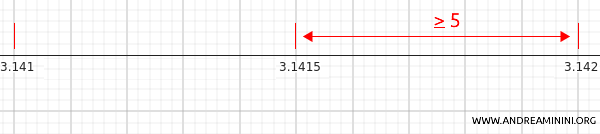
  Note. Here, \( 3.141 \) and \( 3.142 \) are both equally close to \( 3.1415 \). By convention, if the last omitted digit is 5 or more, the next higher value is chosen, yielding \( 3.142 \).

  By contrast, rounding \( \pi = 3.1415926... \) to two decimal places gives \( \pi \approx 3.14 \) because the first omitted digit is 1 (i.e.,  \( \pi = 3.14\color{red}{1}5926... \)), which is less than 5, so it rounds down to \( 3.14 \).
  
  Here, it’s clear that \( 3.141 \) is closer to \( 3.14 \) than to \( 3.15 \).

Truncation and rounding provide practical ways to handle numbers with precision, while keeping results manageable.

Key Differences Between Truncation and Rounding

In general, truncation always results in a lower approximation, never exceeding the actual number.

Rounding, however, provides either a lower approximation if the first omitted digit is less than 5, or a higher one if the digit is 5 or greater.

Note. Choosing between truncation and rounding depends on the specific accuracy needed for calculations and the context. When a lower estimate is required, truncation is preferred, whereas rounding works best for a closer approximation to the actual value.

Pros and Cons of Truncation and Rounding

Both methods have their benefits and drawbacks:

Truncation

• Pros. Truncation is quick and easy to apply, simply cutting off digits beyond a certain point with no extra steps. It ensures the result is always equal to or less than the original number, making it suitable for “conservative estimates” (downward approximations).
• Cons. The main downside is reduced precision. Cutting off decimal digits can make the result less accurate, especially if the removed digits are near halfway. Truncation also risks cumulative and propagated errors, as in repeated operations where truncated sums can yield increasingly inaccurate results.

Rounding

• Pros. Rounding tends to yield greater accuracy by selecting the closest value, preserving more of the original number’s precision. This makes rounding useful in repeated calculations, as it balances upward and downward rounding errors to minimize overall deviation.
• Cons. Rounding requires an additional check of the omitted digit, adding complexity to the process. Rounding may result in a value slightly above the original, which can be undesirable in cases where exceeding the real value is problematic (e.g., calculating an airplane’s fuel range).

And so forth.