Exponential Function Analysis Exercise 11

In this exercise, we analyze the behavior of the exponential function

$$ f(x) = \frac{x}{e^x} $$

We begin by determining its domain.

Domain

The exponential function $ e^x $ is never zero for any real number. Therefore, the domain of $ f(x) $ is the entire real line:

$$ D_f = ( -\infty , \infty ) $$

Points of Discontinuity

The function is defined and continuous over all real numbers, so it has no points of discontinuity.

Horizontal Asymptotes

We first examine the behavior of the function as $ x \to +\infty $:

$$ \lim_{x \to \infty} \frac{x}{e^x} = \frac{\infty}{\infty} $$

This is an indeterminate form. To evaluate the limit, we apply L’Hôpital’s Rule:

$$ \lim_{x \to \infty} \frac{1}{e^x} = 0^+ $$

Therefore, the function tends to zero as $ x \to +\infty $:

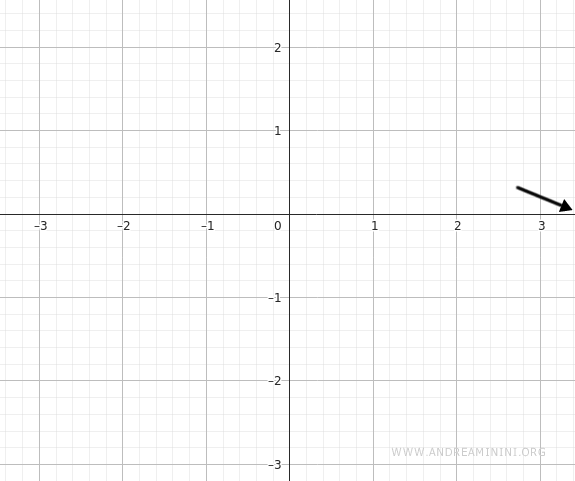
the function approaches zero as x increases

Now we consider the limit as $ x \to -\infty $:

$$ \lim_{x \to -\infty} \frac{x}{e^x} = \frac{-\infty}{0^+} = -\infty $$

So the function diverges to negative infinity as $ x \to -\infty $.

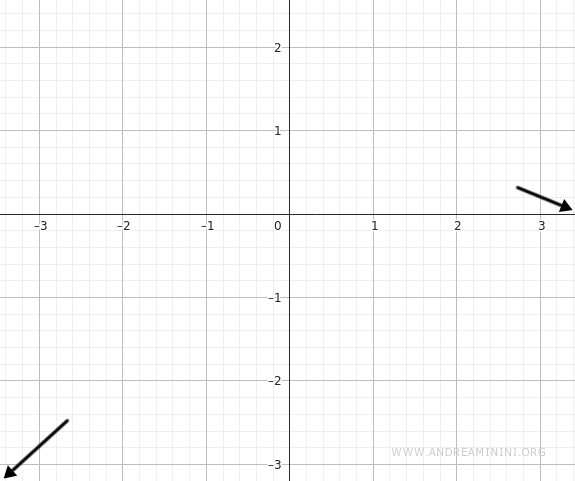
asymptotic behavior as x goes to negative infinity

Vertical Asymptotes

Since the function is defined for all real values of $ x $, there are no vertical asymptotes.

Intercepts

To find the y-intercept, we evaluate the function at $ x = 0 $:

$$ f(0) = \frac{0}{e^0} = \frac{0}{1} = 0 $$

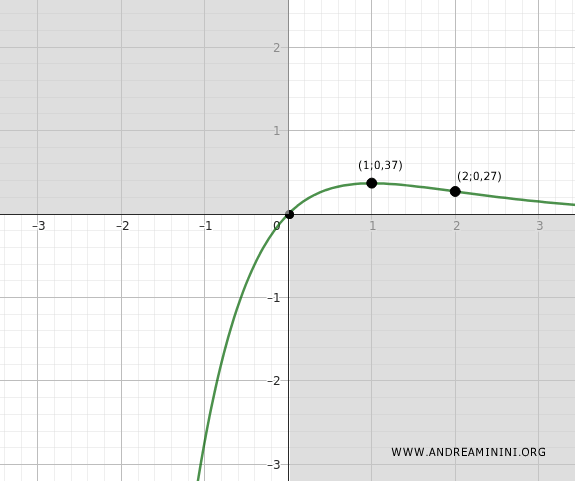
Thus, the graph passes through the origin: (0, 0)

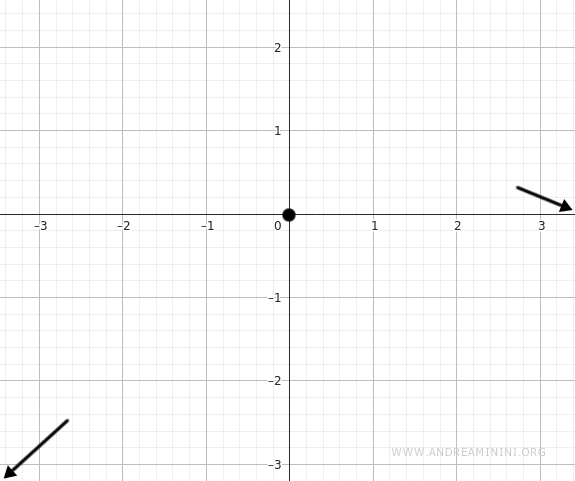
the graph passes through the origin

To find any x-intercepts, we solve:

$$ \frac{x}{e^x} = 0 $$

Multiplying both sides by $ e^x $:

$$ x = 0 $$

The function intersects the x-axis only at the origin.

Sign Analysis

We now analyze the sign of the function:

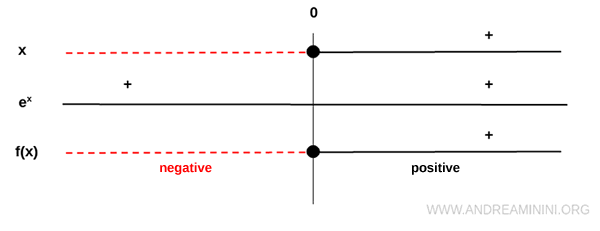
analysis of the function’s sign

The denominator $ e^x $ is always positive, while the numerator $ x $ is positive only when $ x > 0 $.

Therefore, $ f(x) $ is negative for $ x < 0 $, and positive for $ x > 0 $.

This allows us to exclude the quadrants the function cannot occupy.

graph construction based on sign

Increasing and Decreasing Behavior

To determine where the function is increasing or decreasing, we compute its first derivative:

$$ f'(x) = D_x\left[ \frac{x}{e^x} \right] = \frac{e^x - x e^x}{(e^x)^2} = \frac{1 - x}{e^x} $$

Alternatively, expressing the function as $ f(x) = x \cdot e^{-x} $, we can apply the product rule: $$ f'(x) = D_x[x] \cdot e^{-x} + x \cdot D_x[e^{-x}] = e^{-x} - x e^{-x} = e^{-x}(1 - x) = \frac{1 - x}{e^x} $$

Now we examine the sign of $ f'(x) $:

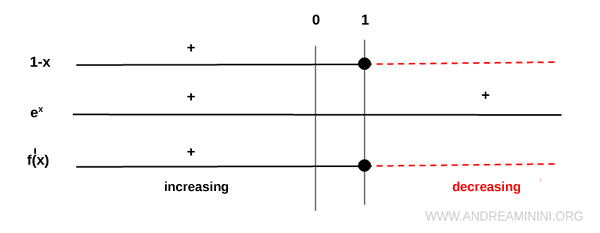
sign analysis of the first derivative

The derivative is positive when $ x < 1 $ and negative when $ x > 1 $, so the function increases on $ (-\infty, 1) $ and decreases on $ (1, \infty) $.

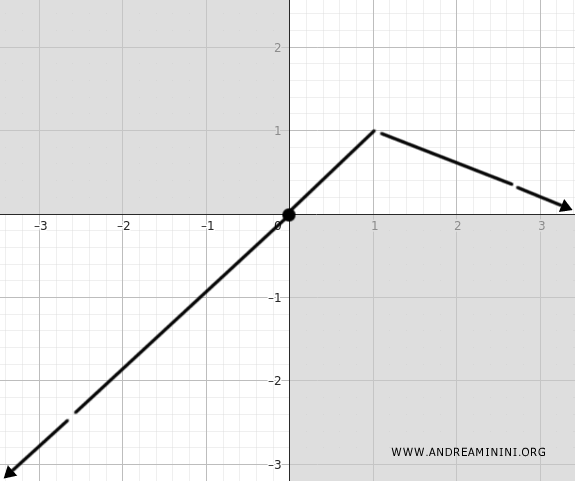
increasing and decreasing intervals

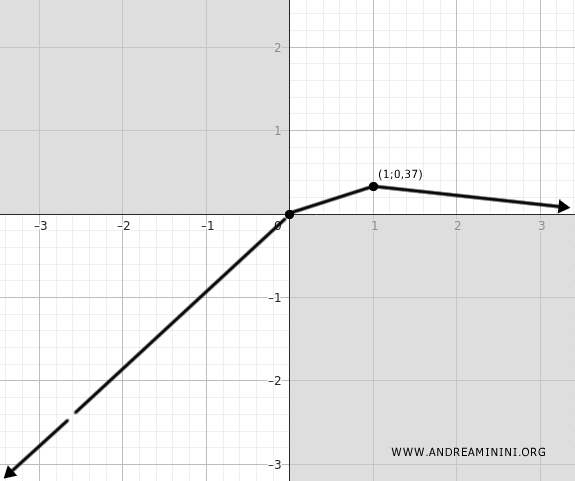
At $ x = 1 $, the derivative vanishes and changes sign from positive to negative. Therefore, the function attains a local maximum at that point.

To find its coordinates, evaluate the function at $ x = 1 $:

$$ f(1) = \frac{1}{e} \approx 0.37 $$

The local maximum occurs at (1, 0.37).

local maximum at x = 1

Concavity, Convexity, and Inflection Points

To study the concavity of the function and locate possible inflection points, we compute the second derivative:

$$ f''(x) = D_x\left[ \frac{1 - x}{e^x} \right] = \frac{-e^x - (1 - x) e^x}{(e^x)^2} $$

$$ = \frac{-2e^x + x e^x}{(e^x)^2} = \frac{e^x(x - 2)}{(e^x)^2} = \frac{x - 2}{e^x} $$

We now analyze the sign of the second derivative:

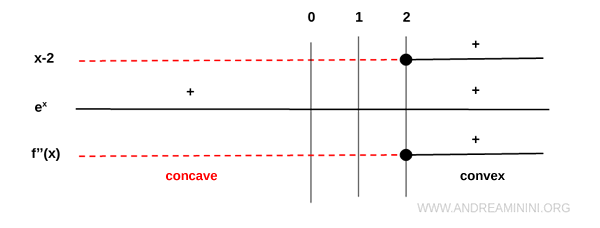
concavity and inflection point analysis

The second derivative is negative for $ x < 2 $ (indicating concavity) and positive for $ x > 2 $ (indicating convexity).

function nearing completion

At $ x = 2 $, $ f''(x) = 0 $ and changes sign, so an inflection point occurs there.

To find the y-coordinate, evaluate the function at $ x = 2 $:

$$ f(2) = \frac{2}{e^2} \approx 0.27 $$

The point of inflection is at (2, 0.27).

inflection point at x = 2

And the analysis continues.