Function Analysis Exercise 10

In this exercise, we analyze the exponential function using standard techniques from calculus:

$$ f(x)= e^{- \frac{1}{x}} $$

Domain

The function is defined for all real numbers except $ x = 0 $:

$$ D_f = \mathbb{R} \setminus \{ 0 \} $$

This exclusion arises because the exponent $ \frac{1}{x} $ is undefined at zero due to division by zero.

Intercepts

Let’s now check whether the graph of the function intersects the coordinate axes:

y-intercept
Since the function is undefined at $ x = 0 $, there is no y-intercept.
x-intercept
To determine if the graph crosses the x-axis, we solve: $$ f(x) = 0 \Rightarrow e^{- \frac{1}{x}} = 0 $$ Taking the natural logarithm of both sides: $$ \ln\left(e^{- \frac{1}{x}}\right) = \ln(0) $$ $$ -\frac{1}{x} = \ln(0) $$ However, $ \ln(0) $ is undefined. Hence, this equation has no solution, and the function does not intersect the x-axis.

Conclusion: The function does not intersect either axis.

Sign

The sign of the function is easy to determine. The exponential function is always positive, so:

$$ f(x) = e^{- \frac{1}{x}} > 0 \quad \forall x \in D_f $$

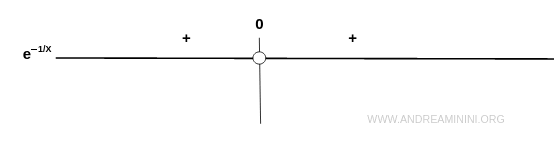
the function is always positive

This means the graph lies entirely in the first and second quadrants of the Cartesian plane.

initial sketch of the graph

Vertical Asymptotes

We examine the behavior near the discontinuity at $ x = 0 $:

As $ x \to 0^- $, the exponent $ -\frac{1}{x} \to +\infty $, so:

$$ \lim_{x \to 0^-} e^{- \frac{1}{x}} = \infty $$

As $ x \to 0^+ $, $ -\frac{1}{x} \to -\infty $, and hence:

$$ \lim_{x \to 0^+} e^{- \frac{1}{x}} = 0 $$

Since the left and right limits are not equal, the function has a discontinuity at $ x = 0 $ but no vertical asymptote.

behavior around x = 0

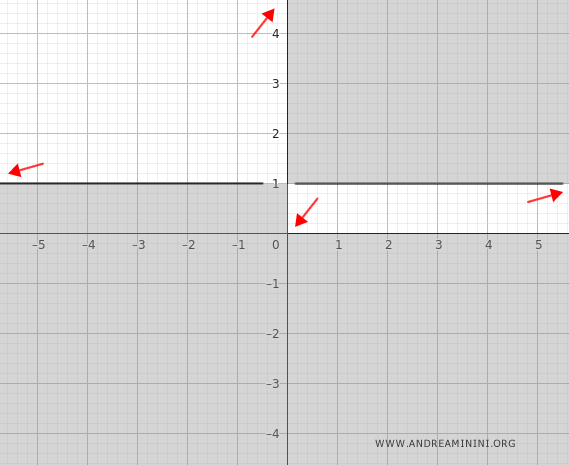
Horizontal Asymptotes

We now consider the behavior as $ x \to \pm \infty $:

As $ x \to +\infty $:

$$ \lim_{x \to +\infty} e^{- \frac{1}{x}} = \frac{1}{e^{\frac{1}{x}}} \to \frac{1}{1} = 1^- $$

Explanation: As $ x $ grows large, $ \frac{1}{x} \to 0^+ $, and since $ e^{\frac{1}{x}} > 1 $, we have $ \frac{1}{e^{1/x}} < 1 $.

As $ x \to -\infty $:

$$ \lim_{x \to -\infty} e^{- \frac{1}{x}} = \frac{1}{e^{\frac{1}{x}}} \to \frac{1}{1} = 1^+ $$

Explanation: Now $ \frac{1}{x} \to 0^- $, so $ e^{\frac{1}{x}} < 1 $, and therefore $ \frac{1}{e^{1/x}} > 1 $.

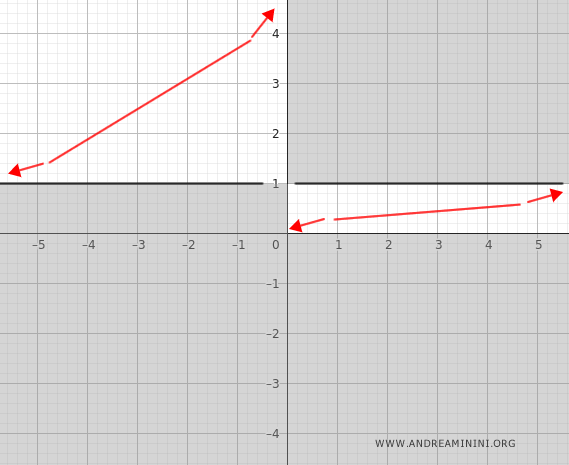
Conclusion: The function has a horizontal asymptote at $ y = 1 $.

graph with horizontal asymptote

Monotonicity

To study the function's increasing/decreasing behavior, we compute the first derivative:

$$ f'(x) = \frac{d}{dx} \left( e^{- \frac{1}{x}} \right) = e^{- \frac{1}{x}} \cdot \frac{1}{x^2} $$

sign of the first derivative

Since both factors are strictly positive, $ f'(x) > 0 $ on the entire domain.

Therefore, the function is strictly increasing for all $ x \in D_f $.

increasing behavior of the graph

Concavity and Inflection Points

Now we study the concavity by computing the second derivative:

$$ f''(x) = \frac{d}{dx} \left( x^{-2} \cdot e^{- \frac{1}{x}} \right) $$

Using the product rule:

$$ f''(x) = -2x^{-3} \cdot e^{- \frac{1}{x}} + x^{-2} \cdot \left( \frac{1}{x^2} \cdot e^{- \frac{1}{x}} \right) $$

$$ f''(x) = e^{- \frac{1}{x}} \cdot \left( -2x^{-3} + x^{-4} \right) $$

Factoring gives:

$$ f''(x) = e^{- \frac{1}{x}} \cdot x^{-3} \cdot \left( -2 + \frac{1}{x} \right) $$

$$ f''(x) = e^{- \frac{1}{x}} \cdot \frac{1 - 2x}{x^4} $$

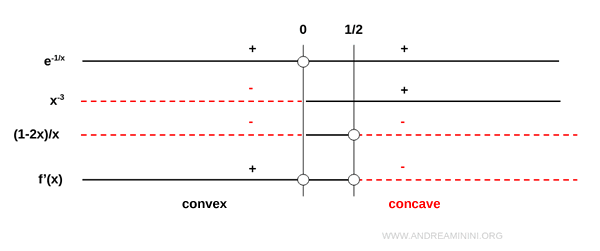
sign of the second derivative

Note: The sign of the second derivative depends on the rational expression $ \frac{1 - 2x}{x} $. It is positive when $ 0 < x < \frac{1}{2} $.

Thus, we conclude:

The function is concave upward (convex) on $ (-\infty, \frac{1}{2}) $
The function is concave downward on $ (\frac{1}{2}, +\infty) $

At $ x = \frac{1}{2} $, the second derivative changes sign, indicating a point of inflection.

This allows us to complete the function's graph:

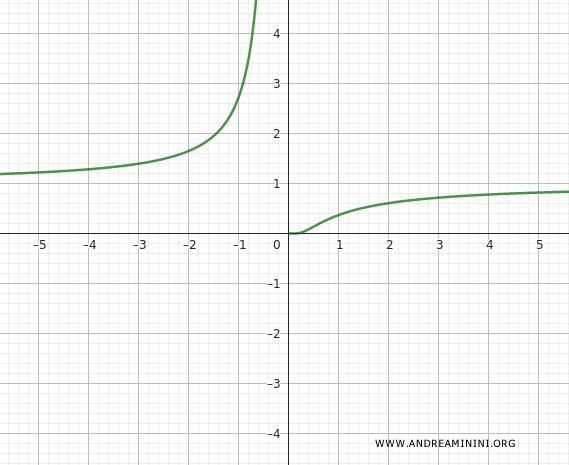
final graph of the function

And that concludes the analysis.