Function Analysis Exercise 7
We’re analyzing the exponential function
$$ e^x + e^{-x} $$
Let’s begin by determining its domain.
Domain
To better understand the domain, I’ll rewrite the function in a more convenient algebraic form:
$$ f(x) = e^x + e^{-x} $$
$$ f(x) = e^x + \frac{1}{e^x} $$
$$ f(x) = \frac{e^x \cdot e^x + 1}{e^x} $$
$$ f(x) = \frac{e^{2x} + 1}{e^x} $$
We now have a rational expression. Since the exponential function is always positive, the denominator never vanishes. As a result, the function is defined for all real values of \( x \).
The domain is the entire set of real numbers:
$$ D_f = \mathbb{R} $$
Sign Analysis
The function \( f(x) = \frac{e^{2x} + 1}{e^x} \) is strictly positive over \( \mathbb{R} \), since both the numerator and denominator are positive for all real numbers.
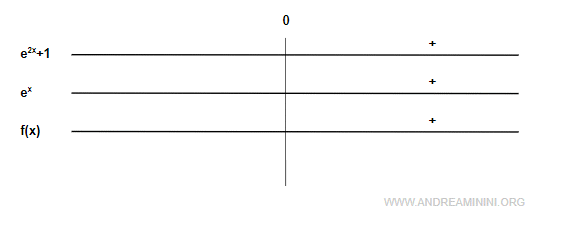
x-intercepts
From the sign analysis, we know that the function is never zero, and therefore it does not intersect the x-axis. Still, for completeness, let’s verify this analytically.
We solve the equation \( f(x) = 0 \):
$$ \frac{e^{2x} + 1}{e^x} = 0 $$
Multiply both sides by \( e^x \):
$$ (e^{2x} + 1) = 0 $$
$$ e^{2x} = -1 $$
This equation has no real solution, since the exponential function is always positive and never equals a negative number.
Therefore, the function has no x-intercepts.
y-intercept
To find the y-intercept, evaluate the function at \( x = 0 \):
$$ f(x) = \frac{e^{2x} + 1}{e^x} $$
$$ f(0) = \frac{e^0 + 1}{e^0} = \frac{1 + 1}{1} = 2 $$
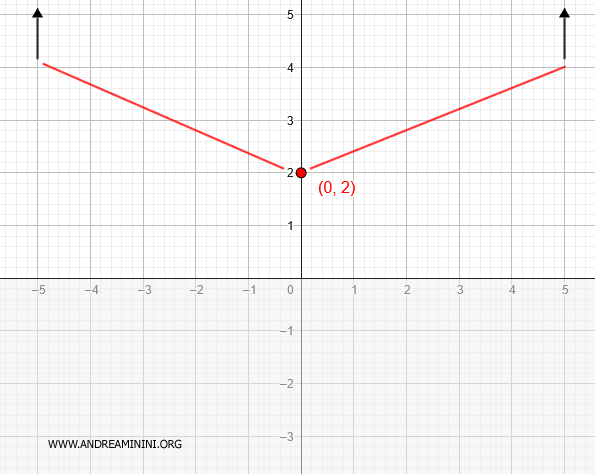
So the graph intersects the y-axis at the point \( (0, 2) \).
This helps establish a key reference point for sketching the graph.
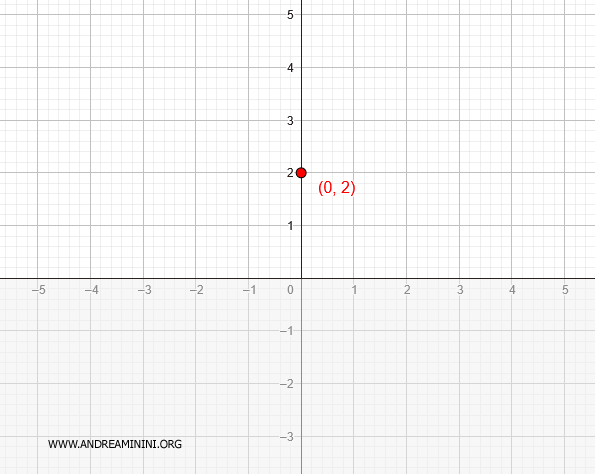
Asymptotes
The function is continuous and defined everywhere in its domain, so there are no vertical asymptotes.
To check for horizontal asymptotes, examine the limits as \( x \to \pm\infty \):
As \( x \to +\infty \):
$$ \lim_{x \to \infty} \left(e^x + e^{-x}\right) = \infty + 0 = \infty $$
As \( x \to -\infty \):
$$ \lim_{x \to -\infty} \left(e^x + e^{-x}\right) = 0 + \infty = \infty $$
So the function diverges in both directions and has no horizontal asymptotes.
Increasing and Decreasing Intervals
To determine where the function is increasing or decreasing, we compute the first derivative and analyze its sign.
Using the simplified form \( f(x) = e^x + e^{-x} \):
$$ f'(x) = \frac{d}{dx}(e^x) + \frac{d}{dx}(e^{-x}) = e^x - e^{-x} $$
Note: We would obtain the same result using the rational form, though with more steps: $$ f'(x) = \frac{d}{dx}\left(\frac{e^{2x} + 1}{e^x}\right) $$ Apply the quotient rule: $$ f'(x) = \frac{(2e^{2x}) \cdot e^x - (e^{2x} + 1) \cdot e^x}{(e^x)^2} $$ $$ = \frac{2e^{3x} - e^{3x} - e^x}{e^{2x}} = \frac{e^{3x} - e^x}{e^{2x}} $$ Factor and simplify: $$ = \frac{e^x(e^{2x} - 1)}{e^{2x}} = \frac{e^{2x} - 1}{e^x} $$
So we can express the derivative as:
$$ f'(x) = \frac{e^{2x} - 1}{e^x} $$
The numerator is negative for \( x < 0 \) and positive for \( x > 0 \), while the denominator is always positive.
Hence, the derivative is:
- Negative on \( (-\infty, 0) \) → function is decreasing
- Positive on \( (0, \infty) \) → function is increasing
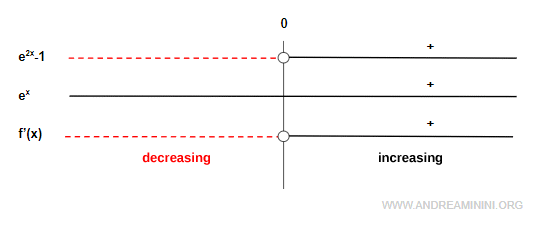
We now update the graph to reflect this monotonicity.
Local Extrema
Critical points occur where the first derivative is zero:
$$ f'(x) = 0 \Rightarrow e^x = e^{-x} $$
Take natural logs of both sides:
$$ \log(e^x) = \log(e^{-x}) \Rightarrow x = -x \Rightarrow 2x = 0 \Rightarrow x = 0 $$
So \( x = 0 \) is a critical point.
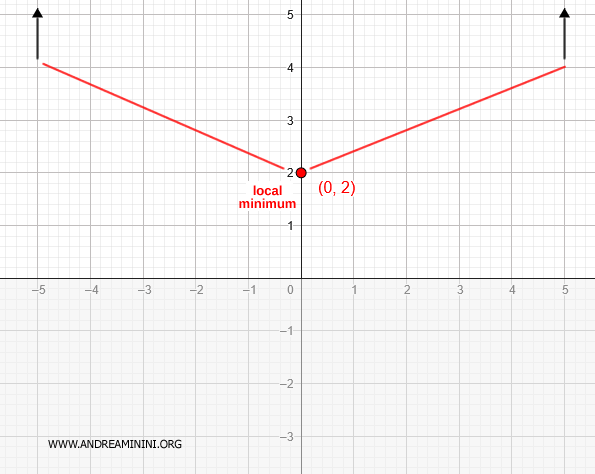
Since the function switches from decreasing to increasing at \( x = 0 \), this is a local minimum.

Evaluating the function at this point:
$$ f(0) = e^0 + e^0 = 1 + 1 = 2 $$
Therefore, the function has a local minimum at the point (0, 2).
Concavity and Convexity
To determine concavity, we compute the second derivative. Using the simpler form:
$$ f''(x) = \frac{d}{dx}(e^x - e^{-x}) = e^x + e^{-x} $$
Which can also be rewritten as:
$$ f''(x) = \frac{e^{2x} + 1}{e^x} $$
This expression is strictly positive for all real numbers.
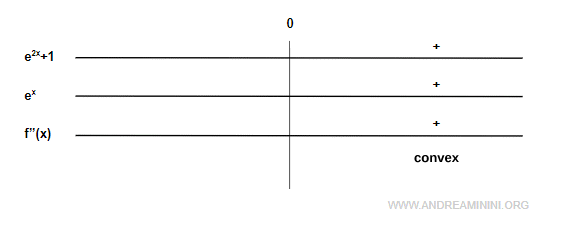
Therefore, the function is strictly convex across its entire domain.
This concludes the complete analysis and sketch of the graph.

And so on.
