Function Analysis Exercise 8

We are analyzing the exponential function

$$ f(x) = e^{\frac{1}{x}} $$

using standard methods from differential calculus.

Domain

The function is defined for all real numbers except at $ x = 0 $:

$$ D_f = \mathbb{R} \setminus \{0\} $$

At $ x = 0 $, the exponent $ \frac{1}{x} $ is undefined due to division by zero, making this a point of discontinuity.

Intercepts

Since the function is undefined at $ x = 0 $, it has no y-intercept.

To check for x-intercepts, we solve:

$$ f(x) = e^{\frac{1}{x}} = 0 $$

Taking the natural logarithm of both sides:

$$ \ln\left(e^{\frac{1}{x}}\right) = \ln(0) $$

The left-hand side simplifies to $ \frac{1}{x} $, but since $ \ln(0) $ is undefined, the equation has no solution.

Therefore, the function has no x- or y-intercepts.

Sign

This analysis is immediate: the exponential function is strictly positive throughout its domain.

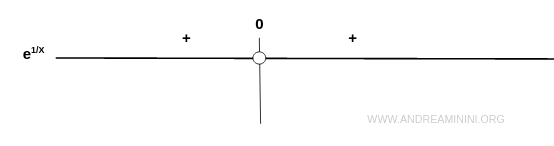
function is positive throughout its domain

Thus, the graph lies entirely within the first and second quadrants.

graph occupies first and second quadrants only

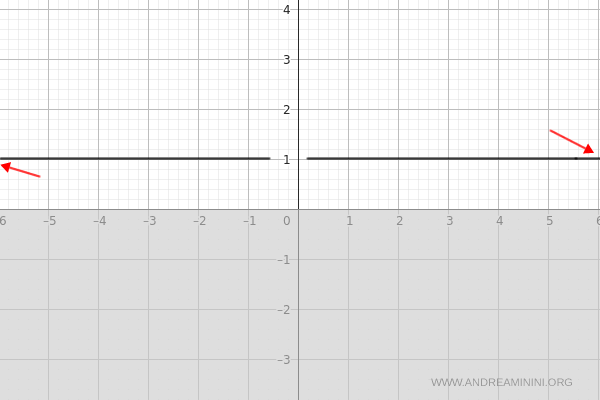
Horizontal Asymptotes

To study end behavior, we evaluate the limits as $ x \to \pm\infty $:

$$ \lim_{x \to \infty} e^{\frac{1}{x}} = 1^+ $$

Note: As $ x \to \infty $, the exponent $ \frac{1}{x} \to 0^+ $, and the function approaches 1 from above.

$$ \lim_{x \to -\infty} e^{\frac{1}{x}} = 1^- $$

Note: As $ x \to -\infty $, the exponent $ \frac{1}{x} \to 0^- $, and the function approaches 1 from below.

Since both one-sided limits converge to the same value, the function has a horizontal asymptote at $ y = 1 $.

horizontal asymptote at y = 1

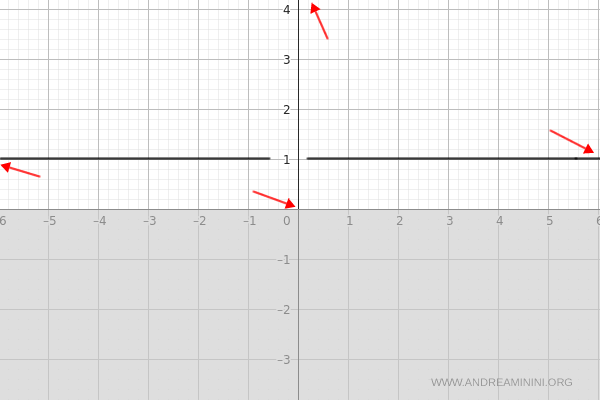
Vertical Asymptotes

Vertical asymptotes can only occur at points of discontinuity. Here, the function is undefined at $ x = 0 $.

Let’s examine the behavior near this point:

$$ \lim_{x \to 0^+} e^{\frac{1}{x}} = +\infty $$

$$ \lim_{x \to 0^-} e^{\frac{1}{x}} = 0 $$

Since the left and right limits do not match, there is no vertical asymptote at $ x = 0 $.

discontinuous behavior near x = 0

Monotonicity

To determine where the function is increasing or decreasing, we compute the first derivative:

$$ f'(x) = \frac{d}{dx}\left(e^{\frac{1}{x}}\right) $$

Using the chain rule:

$$ f'(x) = e^{\frac{1}{x}} \cdot \left(-\frac{1}{x^2}\right) = -\frac{e^{\frac{1}{x}}}{x^2} $$

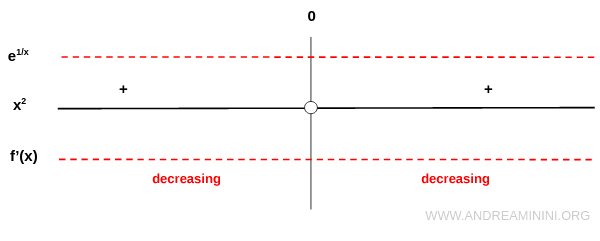
first derivative is negative on both sides of zero

Because $ e^{1/x} > 0 $ and $ x^2 > 0 $ for all $ x \neq 0 $, the derivative is negative throughout the domain.

Hence, the function is strictly decreasing on its entire domain.

function decreases continuously across its domain

Local Extrema

Since the first derivative never vanishes, the function has no local maxima or minima.

Concavity and Inflection Points

To examine concavity, we compute the second derivative:

$$ f''(x) = \frac{d}{dx} \left(-\frac{e^{\frac{1}{x}}}{x^2} \right) $$

Using the quotient rule:

$$ f''(x) = -\frac{ \left( e^{\frac{1}{x}} \cdot \left(-\frac{1}{x^2}\right) \cdot x^2 \right) - \left( e^{\frac{1}{x}} \cdot 2x \right) }{x^4} $$

$$ f''(x) = \frac{ e^{\frac{1}{x}} (1 + 2x) }{x^4} $$

We now analyze the sign of this expression:

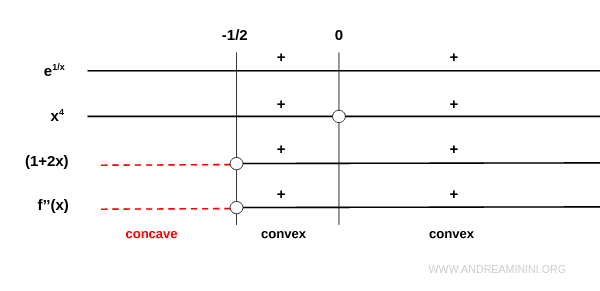
second derivative: inflection point at x = -1/2

This leads us to the following conclusions:

Concave downward on $ (-\infty, -\frac{1}{2}) $
Concave upward on $ (-\frac{1}{2}, \infty) $

At $ x = -\frac{1}{2} $, the concavity changes, so the function has an inflection point.

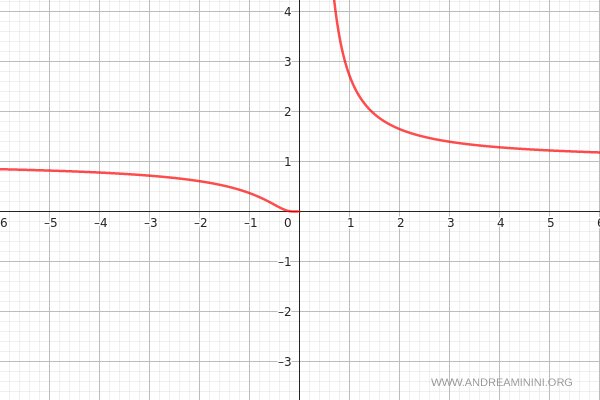
The full graph of the function is shown below:

graph of the function with asymptotes and concavity highlighted

And the analysis continues from here.