Function Analysis Exercise 9
We are tasked with analyzing the function
$$ f(x) = \sqrt{x^2 - 16} $$
using standard methods from differential calculus.
Domain
The function is defined only when the expression under the square root is non-negative:
$$ x^2 - 16 \geq 0 $$
$$ x^2 \geq 16 $$
Taking square roots of both sides (while considering both positive and negative roots):
$$ |x| \geq 4 $$
Which gives the solution set:
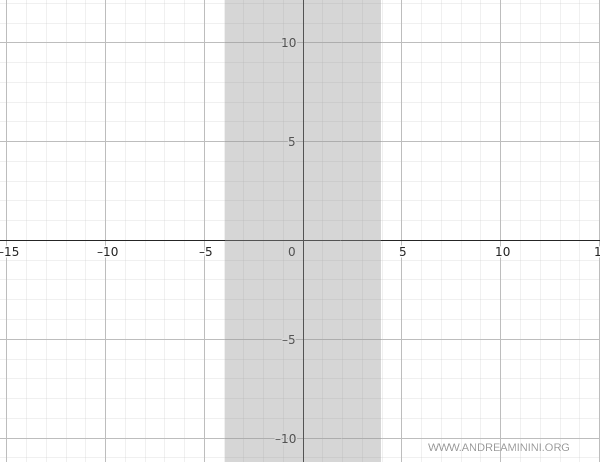
$$ x \in (-\infty, -4] \cup [4, \infty) $$
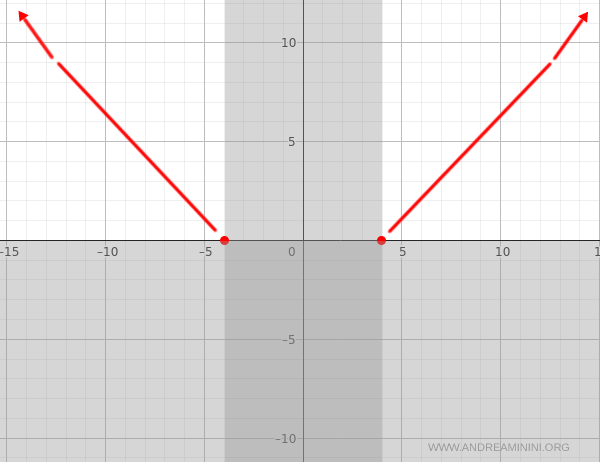
We begin sketching the graph by omitting the interval \( (-4, 4) \), where the function is undefined.
Intercepts
The function has no y-intercept, since it is undefined at \( x = 0 \).
To determine any x-intercepts, we solve:
$$ f(x) = \sqrt{x^2 - 16} = 0 $$
Squaring both sides yields:
$$ x^2 - 16 = 0 \quad \Rightarrow \quad x^2 = 16 $$
Taking square roots:
$$ x = \pm 4 $$
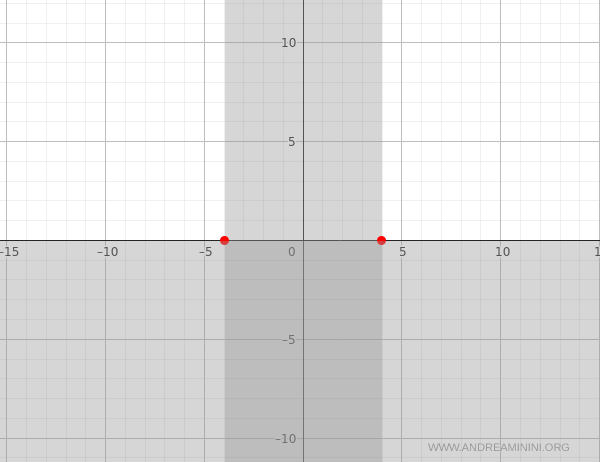
Therefore, the function intersects the x-axis at the points \( (-4, 0) \) and \( (4, 0) \).
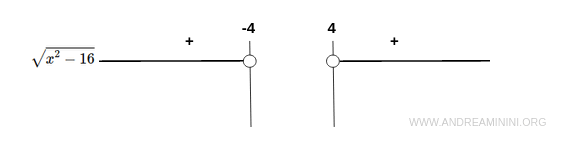
Sign Analysis
The function outputs non-negative values throughout its domain. It is strictly positive except at the endpoints \( x = \pm 4 \), where it evaluates to zero.
Consequently, the graph lies entirely in the upper half of the Cartesian plane. The third and fourth quadrants can be excluded.
Asymptotic Behavior
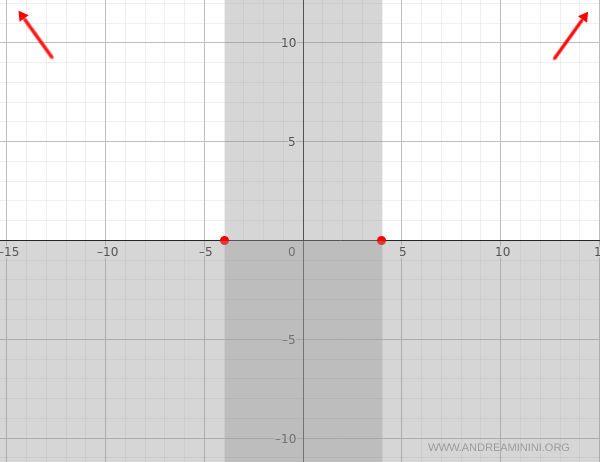
We examine the end behavior of the function as \( x \to \pm\infty \):
$$ \lim_{x \to \infty} \sqrt{x^2 - 16} = \infty \quad \text{and} \quad \lim_{x \to -\infty} \sqrt{x^2 - 16} = \infty $$
In both cases, the function diverges to infinity.
Monotonicity
We compute the first derivative to determine where the function increases or decreases:
$$ f'(x) = \frac{d}{dx} \left[ \sqrt{x^2 - 16} \right] = \frac{x}{\sqrt{x^2 - 16}} $$
We now analyze the sign of the derivative:
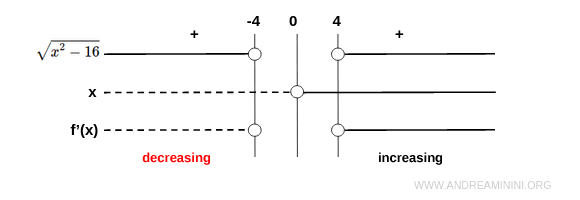
The derivative is negative on \( (-\infty, -4) \), indicating that the function is decreasing in that interval. It is positive on \( (4, \infty) \), where the function increases.
Local Extrema
The first derivative is never zero within the domain of the function, so there are no local maxima or minima in the classical sense.
Concavity and Inflection Points
We now compute the second derivative to study the concavity:
$$ f''(x) = \frac{d}{dx} \left[ \frac{x}{\sqrt{x^2 - 16}} \right] $$
Applying the quotient rule:
$$ f''(x) = \frac{ \sqrt{x^2 - 16} - \frac{x^2}{\sqrt{x^2 - 16}} }{x^2 - 16} $$
Rewriting the numerator as a single fraction:
$$ f''(x) = \frac{ \frac{x^2 - 16 - x^2}{\sqrt{x^2 - 16}} }{x^2 - 16} = \frac{ -16 }{(x^2 - 16) \cdot \sqrt{x^2 - 16}} $$
The second derivative is negative for all values in the domain:
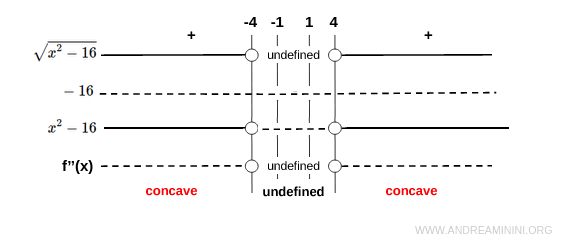
This implies that \( f(x) \) is concave downward on both intervals \( (-\infty, -4] \) and \( [4, \infty) \).

Further analysis could proceed from here.
