Rational Function Analysis Exercise 5

We're tasked with analyzing the graph of the following rational function:

$$ f(x) = \frac{5x-1}{x^2-3x+2} $$

To do this, we'll apply standard tools from calculus, working through each step methodically.

Domain

We begin by determining the domain of the function.

This function is defined for all real values of \( x \), except where the denominator is zero.

The denominator \( x^2 - 3x + 2 \) factors easily, and its roots are:

$$ x = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(1)(2)}}{2(1)} $$

$$ x = \frac{3 \pm \sqrt{9 - 8}}{2} = \frac{3 \pm 1}{2} $$

$$ x = \begin{cases} \frac{2}{2} = 1 \\[0.5em] \frac{4}{2} = 2 \end{cases} $$

Therefore, the domain of \( f \) is:

$$ D_f = (-\infty, 1) \cup (1, 2) \cup (2, \infty) $$

The function is undefined at \( x = 1 \) and \( x = 2 \).

Intercepts

To find the y-intercept, we evaluate the function at \( x = 0 \):

$$ f(0) = \frac{5 \cdot 0 - 1}{0^2 - 3 \cdot 0 + 2} = \frac{-1}{2} $$

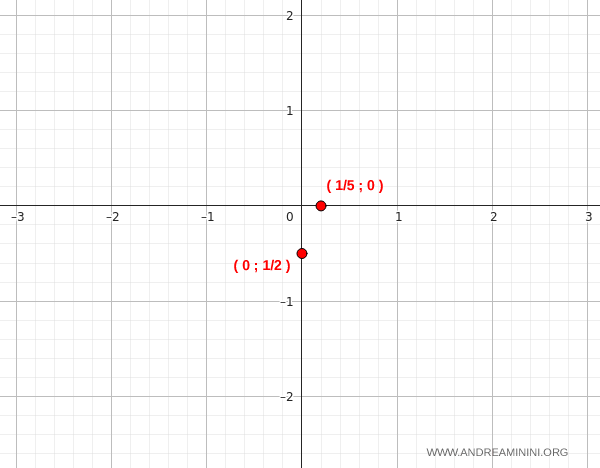
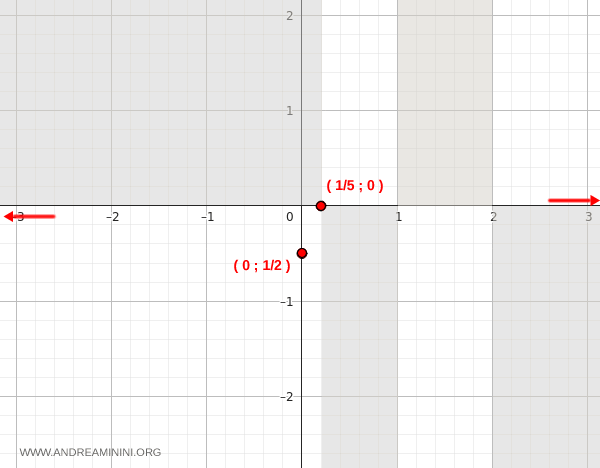
So the graph crosses the y-axis at the point (0, -1/2).

For the x-intercept, we solve \( f(x) = 0 \):

$$ \frac{5x - 1}{x^2 - 3x + 2} = 0 $$

A rational expression is zero when its numerator is zero (as long as the denominator isn't):

$$ 5x - 1 = 0 \quad \Rightarrow \quad x = \frac{1}{5} $$

Thus, the graph intersects the x-axis at (1/5, 0).

We can now mark these two key points on the coordinate plane:

Sign Analysis

Next, we analyze the sign of the function.

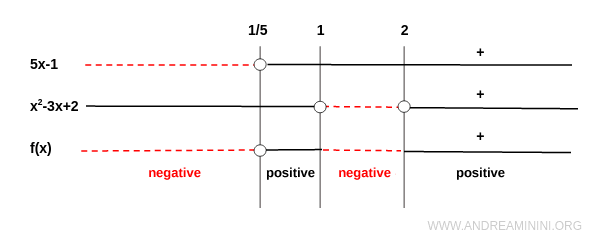
We'll study the signs of the numerator and the denominator separately:

• The numerator \( 5x - 1 \) is positive for \( x > \frac{1}{5} \), zero at \( x = \frac{1}{5} \), and negative for \( x < \frac{1}{5} \).
• The denominator \( x^2 - 3x + 2 \) is a quadratic opening upwards, with roots at \( x = 1 \) and \( x = 2 \). It's positive on \( (-\infty, 1) \cup (2, \infty) \), and negative on \( (1, 2) \).

Combining these results, the function is:

• Negative on \( (-\infty, \frac{1}{5}) \) and \( (1, 2) \)
• Positive on \( (\frac{1}{5}, 1) \) and \( (2, \infty) \)

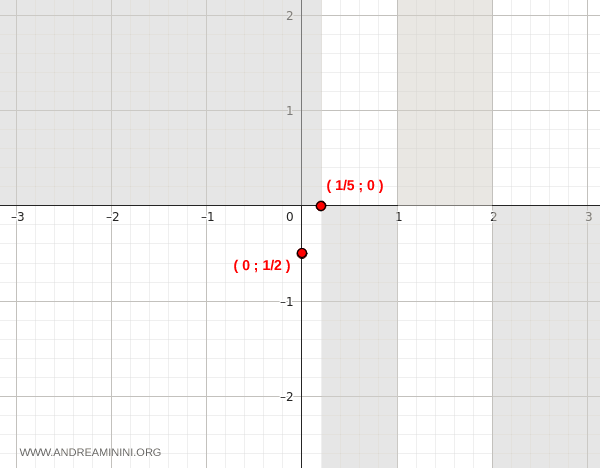
We use this information to exclude the regions of the graph where the function doesn’t exist or takes on inadmissible signs (shaded in gray):

Asymptotes

Horizontal Asymptote

We analyze the behavior of the function as \( x \) tends to infinity:

$$ \lim_{x \to \infty} \frac{5x - 1}{x^2 - 3x + 2} = \frac{\infty}{\infty} $$

This is an indeterminate form, so we apply L’Hôpital’s Rule:

$$ \lim_{x \to \infty} \frac{d}{dx}[5x - 1] \Big/ \frac{d}{dx}[x^2 - 3x + 2] = \lim_{x \to \infty} \frac{5}{2x - 3} = 0^+ $$

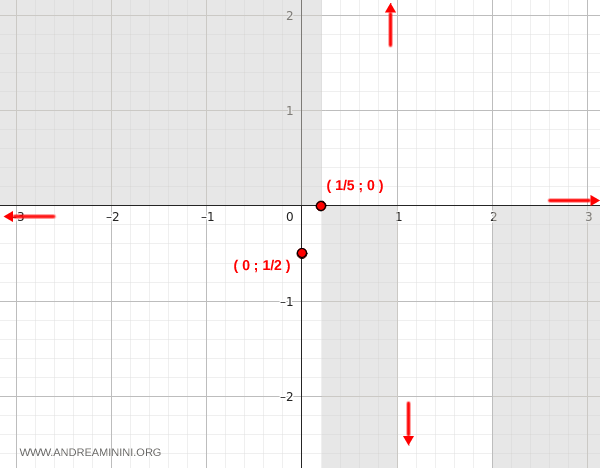
As \( x \to \infty \), the function approaches 0 from above.

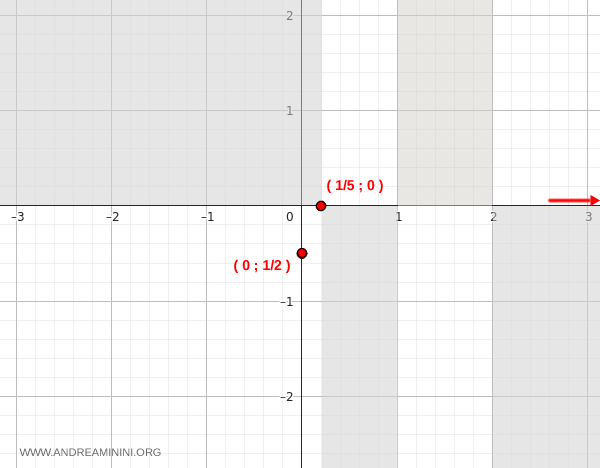
Now consider the behavior as \( x \to -\infty \):

$$ \lim_{x \to -\infty} \frac{5x - 1}{x^2 - 3x + 2} = \frac{-\infty}{\infty} $$

Again, we apply L’Hôpital’s Rule:

$$ \lim_{x \to -\infty} \frac{5}{2x - 3} = 0^- $$

As \( x \to -\infty \), the function approaches 0 from below.

Therefore, the function has a horizontal asymptote along the x-axis: \( y = 0 \).

Vertical asymptote

Vertical asymptotes occur only at points where the function is undefined.

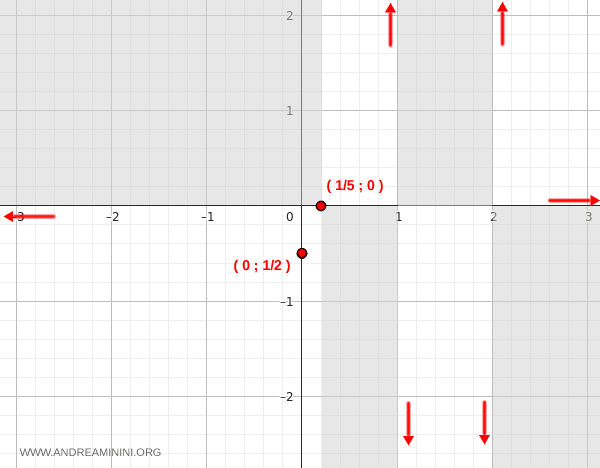
In this case the function is not defined at two points, namely x₁=1 and x₂=2.

To determine whether a vertical asymptote exists at x₁=1, I compute the right-hand and left-hand limits of the function as x approaches 1.

$$ \lim_{x \rightarrow 1^+ } \frac{5x-1}{x^2-3x+2} = \frac{4}{0^+} = -\infty $$

$$ \lim_{x \rightarrow 1^- } \frac{5x-1}{x^2-3x+2} = \frac{4}{0^-} = +\infty $$

A vertical asymptote exists whenever at least one of the two one-sided limits diverges to infinity. In this case both limits diverge, therefore the function has a vertical asymptote at x₁=1.

Next I check whether there is a vertical asymptote at x₂=2 by computing the right-hand and left-hand limits of the function as x approaches 2.

$$ \lim_{x \rightarrow 2^+ } \frac{5x-1}{x^2-3x+2} = \frac{9}{0^+} = +\infty $$

$$ \lim_{x \rightarrow 2^- } \frac{5x-1}{x^2-3x+2} = \frac{9}{0^-} = -\infty $$

Again, at least one of the two limits diverges to infinity, therefore the function has another vertical asymptote at x₂=2.

Increasing and decreasing intervals

To determine the intervals where the function is increasing or decreasing, I compute the first derivative of the function.

$$ f'(x) = D_x \left[ \frac{5x-1}{x^2-3x+2} \right] $$

This is the derivative of a quotient.

$$ f'(x) = \frac{ D[5x-1] \cdot (x^2-3x+2) - (5x-1) \cdot D[x^2-3x+2]}{(x^2-3x+2)^2} $$

$$ f'(x) = \frac{ 5 \cdot (x^2-3x+2) - (5x-1) \cdot (2x-3)}{(x^2-3x+2)^2} $$

$$ f'(x) = \frac{ 5x^2-15x+10 - 10x^2+15x +2x-3}{(x^2-3x+2)^2} $$

Therefore, the first derivative of the function is

$$ f'(x) = \frac{ -5x^2+2x+7}{(x^2-3x+2)^2} $$

I now analyze the sign of the first derivative.

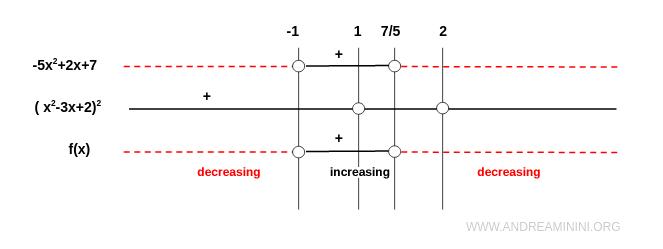
Note. The numerator -5x²+2x+7 is a downward-opening parabola because a=-5<0. Its roots are $$ x = \frac{-2 \pm \sqrt{2^2-4(-5)(7)}}{2(-5)} = \frac{-2 \pm \sqrt{4+140}}{-10} $$ $$ x = \frac{-2 \pm \sqrt{144}}{-10} = \frac{-2 \pm 12}{-10} $$ $$ x = \begin{cases} \frac{-2 - 12}{-10} = \frac{-14}{-10} = \frac{7}{5} \\ \\ \frac{-2 + 12}{-10} = \frac{10}{-10} = -1 \end{cases} $$

Therefore, the function is decreasing on the intervals (-∞,-1) and (7/5,∞), and increasing on the interval (-1,7/5).

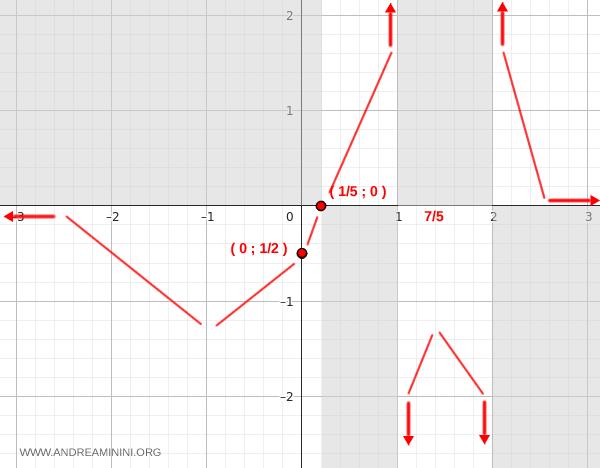
The points where the first derivative is equal to zero, called stationary or critical points, are candidates for local extrema.

In this case the stationary points are x=-1 and x=7/5.

• At the point x=-1 there is a local minimum because the function decreases to the left and increases to the right. Substituting x=-1 into the function gives y=-1. Therefore the local minimum occurs at the coordinates (x;y)=(-1;-1) $$ \frac{5(-1)-1}{(-1)^2-3(-1)+2} =\frac{-6}{6} = -1 $$
• At the point x=7/5 there is a local maximum because the function increases to the left and decreases to the right. Substituting x=7/5 into the function gives y=-25. Therefore the local maximum occurs at the coordinates (x;y)=(7/5;-25) $$ \frac{5(7/5)-1}{(7/5)^2-3(7/5)+2} =\frac{6}{\frac{49}{25}-\frac{21}{5}+2} = \frac{6}{\frac{49-105+50}{25}} = \frac{6}{\frac{-6}{25}} = 6 \cdot \frac{25}{-6} = -25 $$

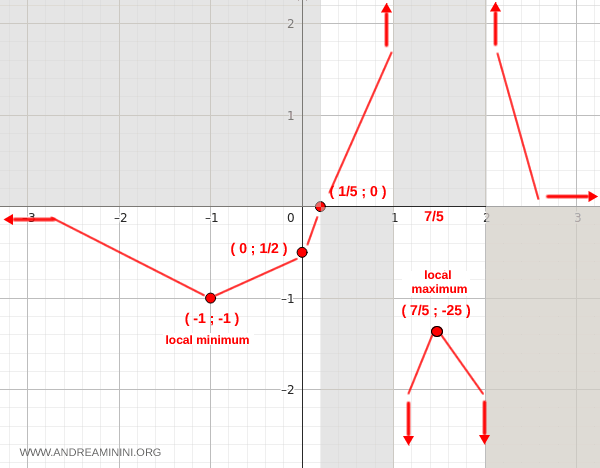
Concavity and convexity

To determine the intervals where the function is concave or convex, I compute the second derivative of the function.

$$ f''(x) = D_x [ f'(x) ] $$

$$ f''(x) = D_x \left[ \frac{ -5x^2+2x+7}{(x^2-3x+2)^2} \right] $$

This is again the derivative of a quotient of functions.

$$ f''(x) = \frac{ D_x[ -5x^2+2x+7 ] \cdot (x^2-3x+2)^2 - ( -5x^2+2x+7 ) \cdot D_x[(x^2-3x+2)^2 ] }{[(x^2-3x+2)^2]^2} $$

$$ f''(x) = \frac{ (-10x+2)\cdot(x^2-3x+2)^2 - (-5x^2+2x+7)\cdot\left(2\cdot(x^2-3x+2)\cdot(2x-3)\right) }{(x^2-3x+2)^4} $$

$$ f''(x) = \frac{ (-10x+2)\cdot(x^2-3x+2)^{\cancel{2}1} - (-5x^2+2x+7)\cdot\left(2\cdot \require{cancel}\cancel{(x^2-3x+2)}\cdot(2x-3)\right) }{(x^2-3x+2)^{\cancel{4}3}} $$

$$ f''(x) = \frac{ (-10x^3+30x^2-20x+2x^2-6x+4) - \\ (-5x^2+2x+7)\cdot(4x-6) }{(x^2-3x+2)^3} $$

$$ f''(x) = \frac{ (-10x^3+32x^2-26x+4) - \\ (-20x^3+30x^2+8x^2-12x+28x-42) }{(x^2-3x+2)^3} $$

$$ f''(x) = \frac{ -10x^3+32x^2-26x+4 +20x^3-30x^2-8x^2+12x-28x+42 }{(x^2-3x+2)^3} $$

$$ f''(x) = \frac{ 10x^3-6x^2-42x+46 }{(x^2-3x+2)^3} $$

In this case the numerator is a cubic polynomial that cannot be simplified further.

However, by evaluating the expression 10x³-6x²-42x+46 in the interval (-2,2), we can observe that it is positive for x>-2 and becomes negative for some value β<-2.

Therefore the sign analysis of the second derivative is the following.

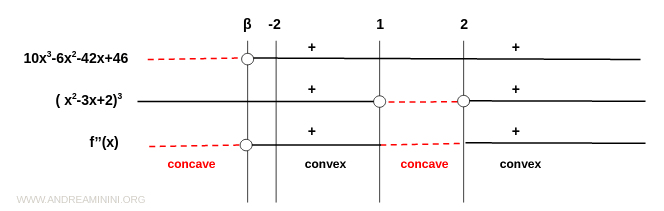
The function f(x) is concave on the interval (-∞,β) where β<-2.

It is then convex on the interval (β,1), concave again on the interval (1,2), and convex again on the interval (2,∞).

In a neighborhood of the point x=β the function is convex to the left and concave to the right. Therefore this point is an inflection point.

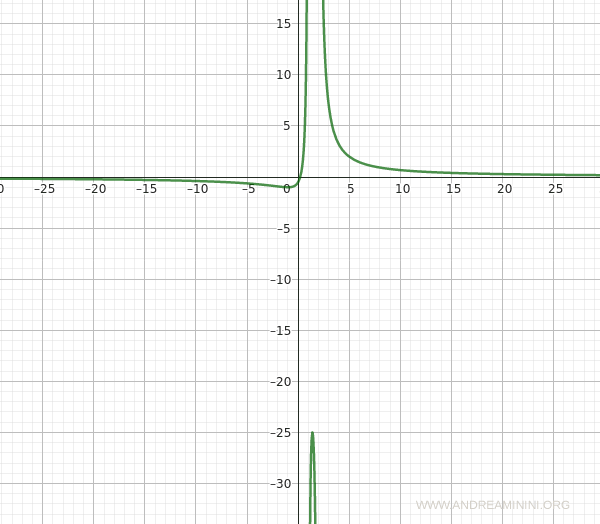
The graph of the function is shown below.

And so on.