Rouché-Capelli Theorem

The Rouché-Capelli theorem gives a rigorous and elegant criterion for determining whether a linear system is consistent and, if so, how many solutions it admits.

A system of linear equations has at least one solution if and only if the rank of the coefficient matrix A matches the rank of the augmented matrix A|B.
$$ rg(A) = rg(A|B) $$

If these ranks differ, the system is inconsistent and therefore has no solutions.

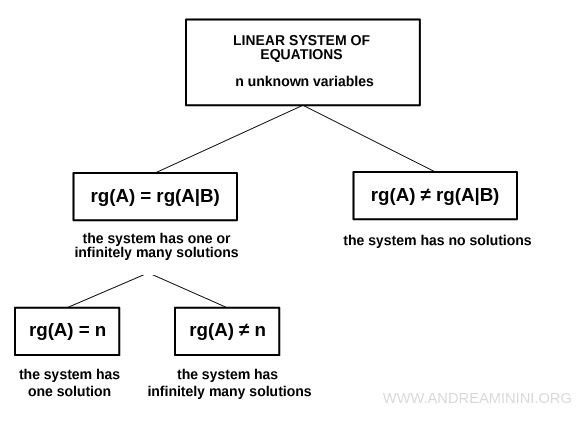
Once consistency is verified, the theorem also indicates the dimension of the solution set, that is, how many solutions the system has.

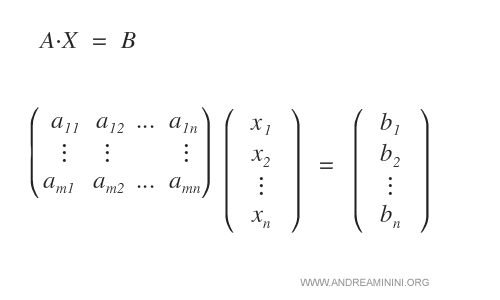
If the system is consistent, the number of solutions corresponds to an infinite family whose dimension is n minus r, where n is the number of unknowns and r is the rank of A. In symbolic form: $$ \infty^{n-r} $$

The Rouché-Capelli theorem is a cornerstone in the theory of linear systems because it distinguishes precisely between systems with no solutions, a unique solution, or infinitely many solutions.

It does not, however, provide the explicit solutions. It merely tells us whether the solution set is empty, a single point, or an affine subspace of higher dimension.

A worked example

Consider the following system, which involves two unknowns (n=2).

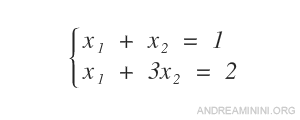
We rewrite the system in matrix form.

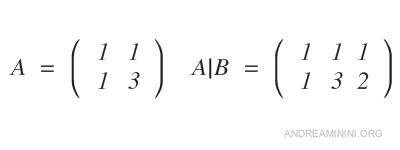
Both matrices have rank two (r), so the system is consistent.

Since n=2 and r=2, the system has exactly one solution.

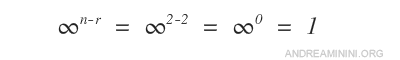
Proof

The system AX = B can be interpreted as expressing the vector B as a linear combination of the column vectors of A.

$$ x_1 \cdot v_1 + ... + x_n \cdot v_n = B $$

Where

• X is the vector of unknowns. $$ X = ( x_1,...,x_n ) $$
• V is the subspace of R^m generated by the column vectors of A. $$ V = ( v_1,...,v_n ) $$
• B is the vector of constant terms. $$ B = ( b_1,...,b_n ) $$

A fundamental result on linear dependence states that the system has a solution if and only if the set {v₁,...,v_n,B} is linearly dependent.

$$ ( v_1 , ... , v_n , B ) $$

This condition is equivalent to requiring that the rank of the augmented matrix A|B coincide with the rank of A.

$$ rg(A|B) = rg(A) $$

In such cases

$$ B \in V $$

Note. If rg(A|B) exceeds rg(A), then v₁,...,v_n,B are linearly independent, the vector B does not belong to the subspace spanned by the columns of A, and the system is inconsistent.

Further remarks

The Rouché-Capelli theorem becomes especially powerful when used alongside Cramer’s rule for square systems.

According to Cramer’s rule, a linear system with a square coefficient matrix has a unique solution if and only if the determinant of A is nonzero (Δ≠0).

If the determinant is zero (Δ=0), the system cannot have a unique solution. It may instead be inconsistent or possess infinitely many solutions. Cramer’s rule alone cannot distinguish between these two possibilities.

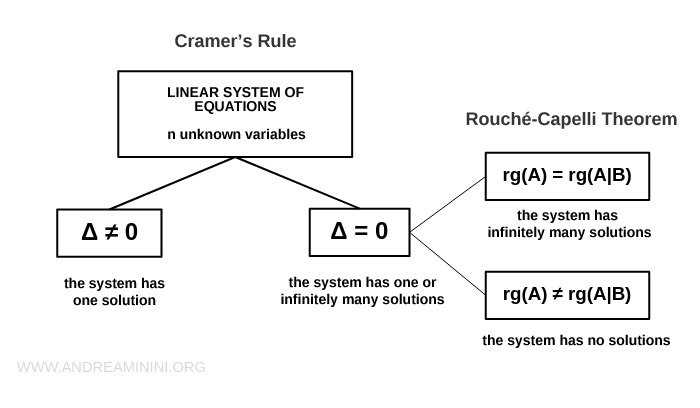
When Δ=0, the Rouché-Capelli theorem allows us to determine whether the solution set is empty or infinite.

By combining both results, we can fully classify the solution set of a linear system.

However, neither Cramer’s rule nor the Rouché-Capelli theorem applies universally.

Cramer’s rule requires the coefficient matrix to be square, so it works only when the number of equations equals the number of unknowns (m=n).

Moreover, the Rouché-Capelli theorem is most efficient for systems of moderate size. For large systems, computing determinants and ranks becomes increasingly demanding.

Note. In practice, for larger or more intricate systems, it is often preferable to use Gauss-Jordan elimination, which reduces the augmented matrix A|B to a row echelon form. This method works for any number of equations and unknowns and avoids the computational overhead of determinants and rank calculations.

And so on.