Worked Example Function Analysis 6

In this example, we will analyze the following function and construct its graph:

$$ f(x) = x^3 - 3x + 2 $$

We will apply standard tools of mathematical analysis to study its behavior.

Domain

The domain of the function is the set of all real numbers:

$$ D_f = \mathbb{R} $$

The function is defined for every real value of x.

Intercepts

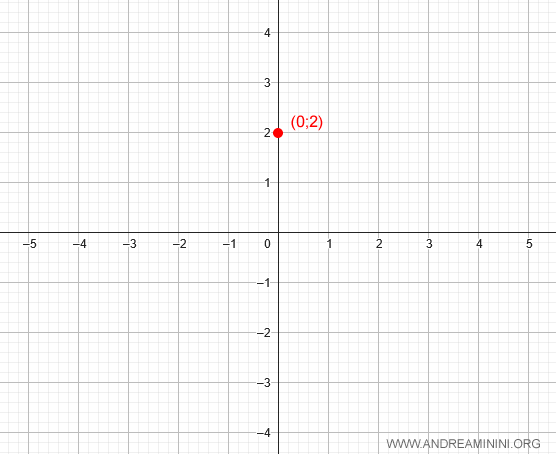
To find the y-intercept, we evaluate the function at x = 0:

$$ y = 0^3 - 3 \cdot 0 + 2 = 2 $$

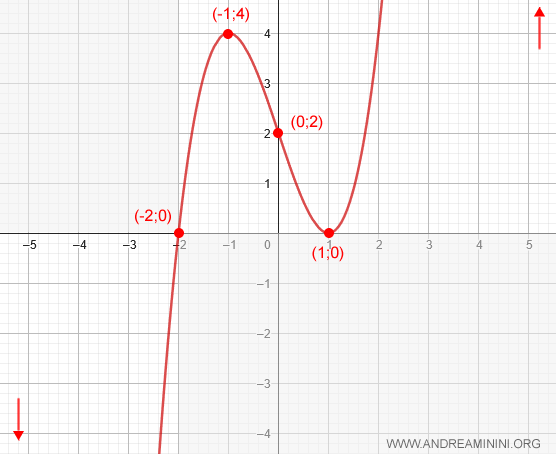
Thus, the graph passes through the point (0, 2):

To find the x-intercepts, we solve:

$$ x^3 - 3x + 2 = 0 $$

We can immediately see that x = 1 is a root. We can then factor the polynomial using Ruffini’s method:

$$ \begin{array}{c|lcc|r} & 1 & 0 & -3 & 2 \\ 1 & & 1 & 1 & -2 \\ \hline & 1 & 1 & -2 & 0 \end{array} $$

This gives the factorization:

$$ (x - 1)(x^2 + x - 2) $$

The first factor vanishes at x = 1. The quadratic factor has roots:

$$ x = \frac{-1 \pm \sqrt{1 - 4(1)(-2)}}{2} $$

$$ x = \frac{-1 \pm \sqrt{9}}{2} $$

$$ x = \frac{-1 \pm 3}{2} $$

$$ x = \begin{cases} \frac{-1 - 3}{2} = -2 \\[6pt] \frac{-1 + 3}{2} = 1 \end{cases} $$

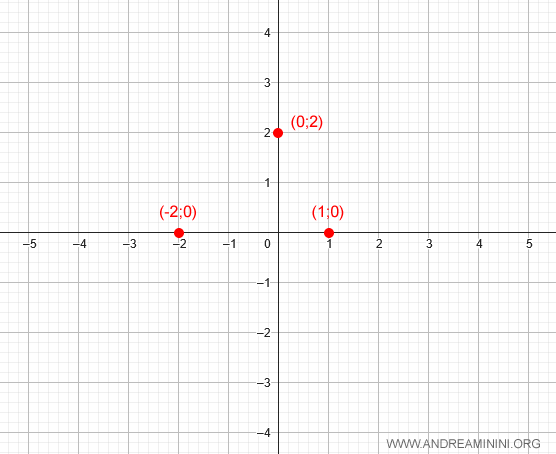
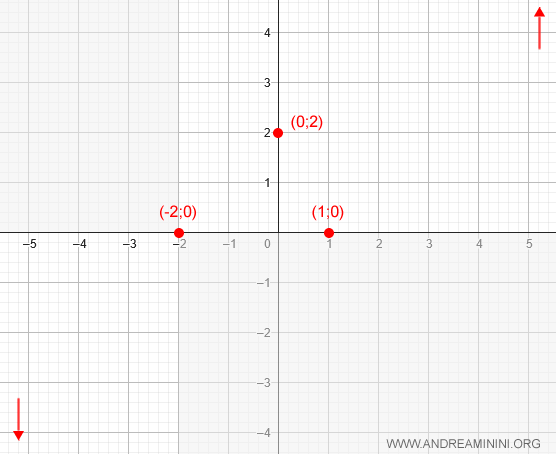
Therefore, the function crosses the x-axis at x = -2 and x = 1, and the graph passes through the points (-2, 0) and (1, 0):

Asymptotes

Since the function is defined everywhere, there are no vertical asymptotes.

To determine whether there are any horizontal asymptotes, we examine the limits as x → ±∞:

$$ \lim_{x \rightarrow +\infty} x^3 - 3x + 2 = +\infty $$

$$ \lim_{x \rightarrow -\infty} x^3 - 3x + 2 = -\infty $$

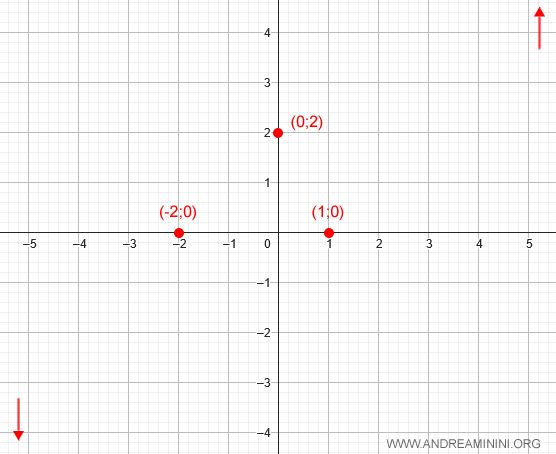
Thus, there are no horizontal asymptotes: the function tends to +∞ as x → +∞ and to -∞ as x → -∞.

We can note this end behavior on the graph as a reference:

Sign Analysis

To analyze the sign of the function, we use the factorized form obtained from Ruffini’s method:

$$ f(x) = (x - 1)(x^2 + x - 2) $$

This makes it easier to analyze the sign:

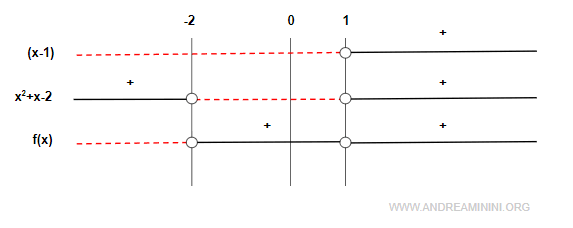
The factor (x - 1) is positive when x > 1, while the quadratic factor is an upward-opening parabola with roots at x = -2 and x = 1.

Therefore, the function is negative on the interval (-∞, -2), and positive on (-2, ∞).

We can now eliminate regions of the Cartesian plane where the function does not appear:

Increasing and Decreasing Intervals

We now compute the first derivative to analyze the intervals of increase and decrease:

$$ f'(x) = D_x[x^3 - 3x + 2] = 3x^2 - 3 $$

Solving for f'(x) > 0:

$$ x^2 > 1 $$

Thus, f'(x) is positive on (-∞, -1) and (1, ∞), and equals zero at x = -1 and x = 1:

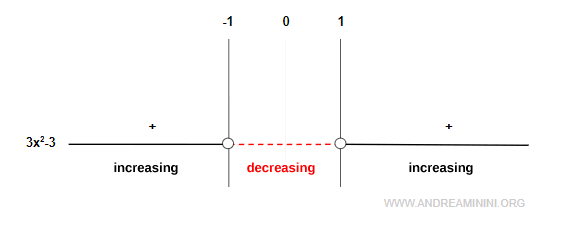
This tells us:

• The function is increasing on (-∞, -1)
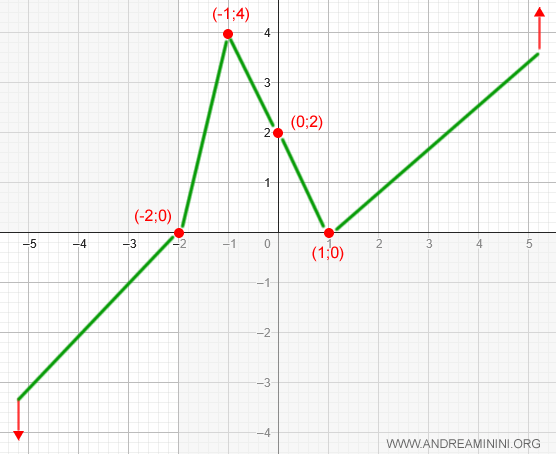
• At x = -1, there is a local maximum since f'(x) = 0 and the function changes from increasing to decreasing.

  Note. To find the coordinates: $$ y = (-1)^3 - 3(-1) + 2 = -1 + 3 + 2 = 4 $$ So the local maximum is at (-1, 4).

• The function is decreasing on (-1, 1)
• At x = 1, there is a local minimum since f'(x) = 0 and the function changes from decreasing to increasing.

  Note. To find the coordinates: $$ y = (1)^3 - 3(1) + 2 = 1 - 3 + 2 = 0 $$ So the local minimum is at (1, 0).

• The function is increasing on (1, ∞)

We can now add this information to the graph:

Concavity and Convexity

To analyze concavity and convexity, we compute the second derivative:

$$ f''(x) = D_x[3x^2 - 3] = 6x $$

The second derivative is negative on (-∞, 0), and positive on (0, ∞):

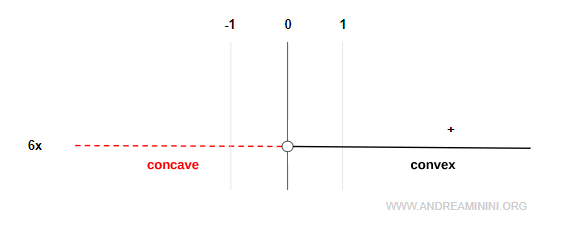
Thus:

• The function is concave on (-∞, 0)
• The function is convex on (0, ∞)

This final piece of information allows us to complete the graph of the function:

And so on.