Finding the Inverse Matrix with Gaussian Elimination

Gaussian elimination offers an alternative approach to computing the inverse of a matrix.

It’s particularly useful when the matrix is large and direct formulas become cumbersome.

Step-by-step: Inverting a matrix with Gaussian elimination

Start by placing the identity matrix I to the right of the matrix M.

This creates an augmented matrix, written as M|I.

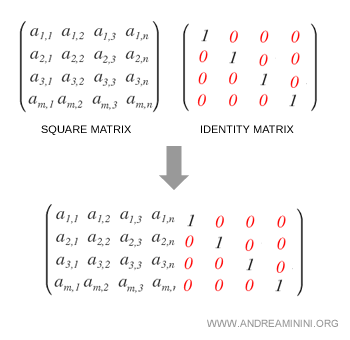
In this augmented matrix, the identity matrix appears on the right-hand side (shown in red).

The goal is to use Gaussian row operations to turn the left block into the identity matrix.

Note. The basic row operations are: swapping two rows, multiplying a row by a nonzero scalar k, and adding a multiple of one row to another.

If the left-hand block becomes the identity, then the block on the right will be the inverse matrix of M.

A worked example

Consider the 2×2 matrix:

$$ M = \begin{pmatrix} 2 & 1 \\ -1 & 1 \end{pmatrix} $$

We want to compute its inverse, M^-1, using Gaussian elimination.

Attach the 2×2 identity matrix on the right:

$$ M|I = \begin{pmatrix} 2 & 1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{pmatrix} $$

Now we’ll transform the left block into the identity matrix by performing row operations.

First, swap the two rows: R1 ⇔ R2

$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ 2 & 1 & 1 & 0 \end{pmatrix} $$

Next, add twice the first row to the second: R2 = R2 + 2·R1

$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ 2 + (-1) \cdot 2 & 1 + 1 \cdot 2 & 1 + 0 \cdot 2 & 0 + 1 \cdot 2 \end{pmatrix} $$

$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ \color{red}0 & 3 & 1 & 2 \end{pmatrix} $$

Now eliminate the entry above the 3 by subtracting one third of the second row from the first: R1 = R1 + (−1/3)·R2

$$ M|I = \begin{pmatrix} -1 - 0 \cdot \frac{1}{3} & 1 - 3 \cdot \frac{1}{3} & 0 - 1 \cdot \frac{1}{3} & 1 - 2 \cdot \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$

$$ M|I = \begin{pmatrix} -1 & \color{red}0 & - \frac{1}{3} & \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$

Multiply the first row by −1: R1 = (−1)·R1

$$ M|I = \begin{pmatrix} -1 \cdot (-1) & 0 \cdot (-1) & - \frac{1}{3} \cdot (-1) & \frac{1}{3} \cdot (-1) \\ 0 & 3 & 1 & 2 \end{pmatrix} $$

$$ M|I = \begin{pmatrix} \color{red}1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$

Finally, divide the second row by 3: R2 = (1/3)·R2

$$ M|I = \begin{pmatrix} 1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 \cdot \frac{1}{3} & 3 \cdot \frac{1}{3} & 1 \cdot \frac{1}{3} & 2 \cdot \frac{1}{3} \end{pmatrix} $$

$$ M|I = \begin{pmatrix} 1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 & \color{red}1 & \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$

At this point, the left-hand block is the identity matrix.

$$ M|I = \begin{pmatrix} \color{red} 1 & \color{red}0 & \frac{1}{3} & - \frac{1}{3} \\ \color{red}0 & \color{red}1 & \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$

So, M is indeed invertible.

The inverse matrix is the block on the right:

$$ M^{-1} = \begin{pmatrix} \frac{1}{3} & - \frac{1}{3} \\ \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$

Note. I also solved this small “toy problem” using other methods for finding inverses, and of course the result came out the same.