General Linear Group
The General Linear Group
In linear algebra, the general linear group (GL) is the set of all invertible matrices of order n over a field K. It is also referred to as the matrix group and is denoted by GL(n,K) or GLn(K).
The concept of the general linear group was first introduced in 1832 by Évariste Galois.
A matrix is invertible if it is non-singular, meaning that its determinant is nonzero.
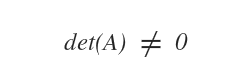
Accordingly, the general linear group (GL) of invertible real matrices of order n is defined as follows:
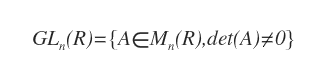
Explanation. Any matrix A of order n with a nonzero determinant belongs to the general linear group GL.
Example
The following matrix is an element of the general linear group of order 2.

Special Linear Group
The special linear group (SL) consists of real square matrices of order n whose determinant is equal to one. It forms a subgroup of GL.
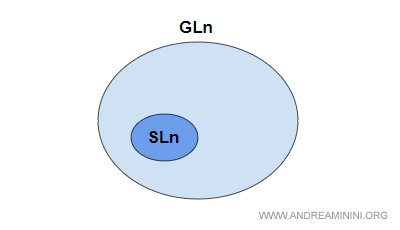
The special linear group is denoted by SL(n,K) or SLn(K).
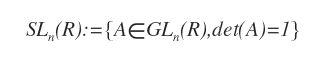
Explanation. Any matrix A in GLn with determinant equal to one also belongs to the special linear group SLn.
Example
The following matrix is an element of the special linear group of order 2.

The Special Orthogonal Group
The special orthogonal group is a subgroup of the special linear group SLn, consisting of real orthogonal matrices of order n with determinant equal to 1.
It is denoted by SOn.

The special orthogonal group can be characterized as the intersection of the special linear group SLn with the set On of orthogonal matrices of order n.
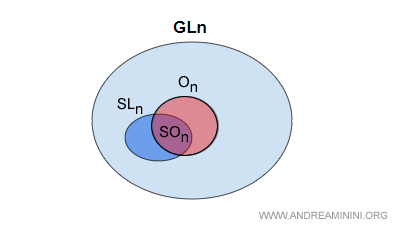
Distinction between the special orthogonal and general orthogonal groups. The special orthogonal group SOn is a subgroup of SLn. The general orthogonal group On, by contrast, consists of all orthogonal matrices with determinant +1 or −1. On is itself a subgroup of the general linear group GLn.
Example
The following matrix is an element of the special orthogonal group SO2 of order 2.

