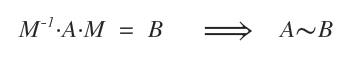Matrices (FAQ)

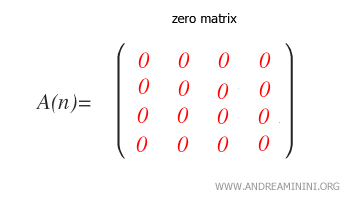
1. What is a zero matrix?
   It is a matrix with all its elements equal to zero.
   
2. What is a square matrix?
   It is a matrix with the same number of rows and columns (m=n).
   
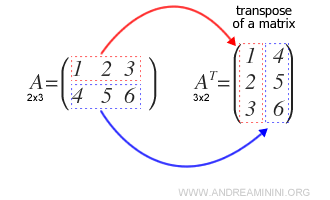
3. What is a transpose matrix?
   A transpose matrix A^T is a matrix obtained by transforming each row into a column.
   
4. What is an opposite matrix?
   It is a matrix -A with all its elements having the same absolute value but opposite algebraic sign compared to a reference matrix A.
   
5. What is an equivalent matrix?
   Two matrices are equivalent if they are associated with linear systems with the same set of solutions.
   
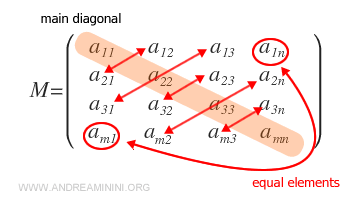
6. What is a symmetric matrix?
   A symmetric matrix is a square matrix with corresponding elements equal (aij=aji).
   
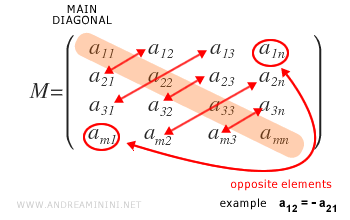
7. What is an antisymmetric matrix?
   An antisymmetric matrix is a square matrix whose corresponding elements are opposite in sign ( a_ij=-a_ji ).
   
8. What is a diagonal matrix?
   It is a square matrix with zeros in all elements except those on the main diagonal, which runs from the top-left to the bottom-right corner. This means that the matrix has no entries above or below the diagonal
   
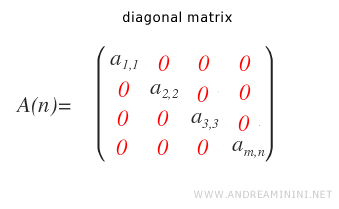
9. What is the identity matrix?
   The identity matrix (or unit matrix) is a diagonal matrix with all elements on the main diagonal equal to one. It is a subset of scalar matrices.
   
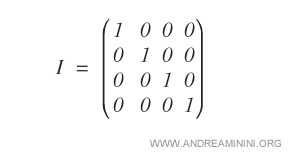
10. What is a scalar matrix?
    A scalar matrix is a square matrix with all elements on the main diagonal equal to each other and greater than zero. For example, here's a scalar matrix:
    
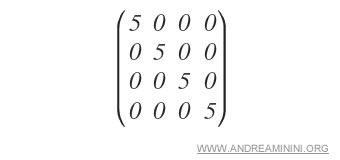
11. What is an invertible matrix?
    An n × n square matrix A is said to be invertible if there exists an n × n square matrix A^-1 of the same order, called the inverse matrix, such that the product A·A^-1 and A^-1·A are equal to the identity matrix I_(n).
    
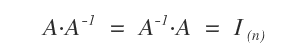
12. What is the orthogonal matrix?
    An invertible matrix A is said to be orthogonal if its transpose A^T is equal to its inverse matrix A^-1.
    
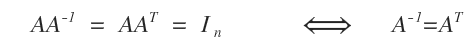
13. What is the determinant?
    The determinant is a number that summarizes the characteristics of a square matrix. It is indicated as det(A) or |A|.
    
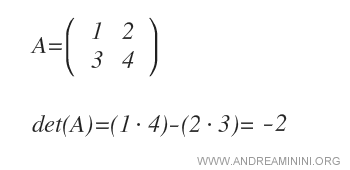
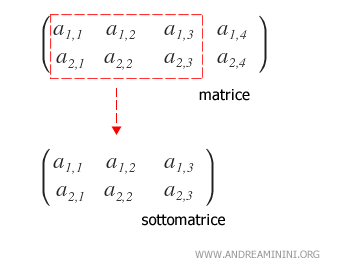
14. What is a submatrix?
    A submatrix is a matrix obtained by eliminating some rows or columns of the original matrix.
    
15. What is a complementary submatrix?
    A complementary submatrix is a lower-order matrix obtained by removing only one row and one column.
    
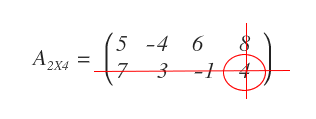
16. What is the minor of a matrix?
    The minor is the determinant of a square submatrix obtained by removing i rows and j columns.
    
17. What is the complementary minor?
    In a square matrix A of order n, the complementary minor is the determinant of a complementary submatrix A_(ij) that is achieved by removing the i-th row and the j-th column from the matrix A. An example of a complementary minor of the element a_ij.
    
18. What is the cofactor?
    The cofactor (algebraic complement) is the corresponding minor of the submatrix A_(ij), multiplied by a scalar (-1)^i+j. It's the corresponding minor calculated with a sign that changes depending on the position of the elements in the submatrix.
    
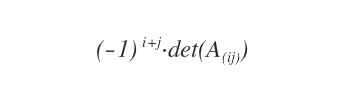
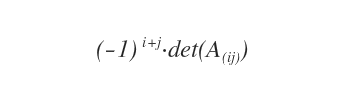
19. What is the adjugate matrix?
    The adjugate matrix is the transpose of the matrix of cofactors.
    
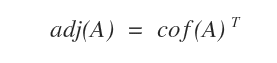
20. What is the trace of a matrix?
    The trace of a matrix is the algebraic sum of the elements on its main diagonal.
    
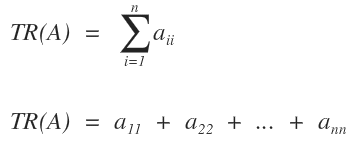
21. What is the rank of a matrix?
    The rank of a matrix is the highest order of any non-zero minor.
22. What is a singularity matrix?
    A square matrix is referred to as singular if its determinant equals zero.
23. What are two similar matrices?
    Two matrices A and B are said to be similar if there exists an invertible matrix such that M^-1AM = B