Step-by-step solution: Analysis of the series $ \sum_{n=2}^{\infty} \frac{n+1}{n-1} $

In this exercise, I’m analyzing the series

\[ \sum_{n=2}^{\infty} \frac{n+1}{n-1} \]

The index starts at 2 to avoid division by zero.

By inspecting the general term, it becomes clear that it can be rewritten in a more manageable form to facilitate the analysis.

I express the numerator $ n+1 $ as $ n - 1 + 2 $, which yields:

$$ \frac{n+1}{n-1} = \frac{n - 1 + 2}{n - 1} $$

$$ \frac{n+1}{n-1} = \frac{(n - 1) + 2}{n - 1} $$

$$ \frac{n+1}{n-1} = \frac{n-1}{n-1} + \frac{2}{n - 1} $$

$$ \frac{n+1}{n-1} = 1 + \frac{2}{n - 1} $$

This allows us to rewrite the original series as:

$$ \sum_{n=2}^{\infty} \left(1 + \frac{2}{n - 1}\right) $$

Now, applying the linearity of summation, we have:

$$ \sum_{n=2}^{\infty} 1 + \sum_{n=2}^{\infty} \frac{2}{n - 1} $$

$$ = \sum_{n=2}^{\infty} 1 + 2 \cdot \sum_{n=2}^{\infty} \frac{1}{n - 1} $$

This representation is more convenient for determining the convergence of the series.

The first sum, $ \sum_{n=2}^{\infty} 1 $, is the infinite sum of the constant 1, which clearly diverges. The second sum, $ \sum_{n=2}^{\infty} \frac{1}{n - 1} $, is the harmonic series shifted by one index (with $ k = n - 1 $), starting at 2 - and it, too, diverges.

Therefore, we conclude that the series diverges.

$$ \sum_{n=2}^{\infty} \frac{n+1}{n-1} = \underbrace{ \sum_{n=2}^{\infty} 1}_{\text{divergent}} + 2 \cdot \underbrace{ \sum_{n=2}^{\infty} \frac{1}{n - 1} }_{\text{divergent}} $$

Hence, the series $ \sum_{n=2}^{\infty} \frac{n+1}{n-1} $ diverges.

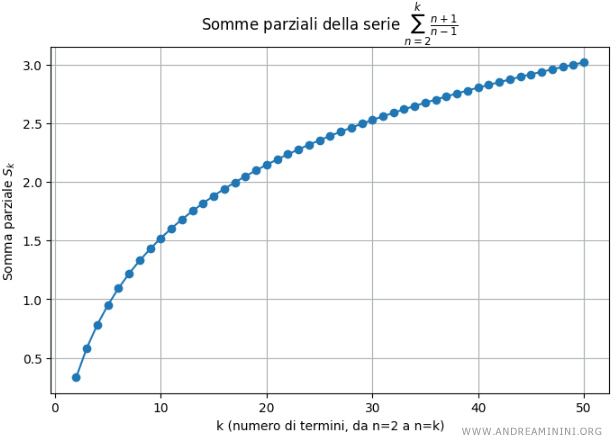
example

And so on.