Exploring the convergence of the series $ \frac{n}{2n+1} $ step-by-step

In this exercise, the goal is to determine the behavior of the series

\[ \sum_{n=1}^{\infty} \frac{n}{2n+1} \]

Determining the behavior of a series means establishing whether it converges - that is, whether it approaches a finite sum - or diverges, meaning the sum is either infinite or undefined.

The first step is to analyze the general term of the series:

\[ a_n = \frac{n}{2n+1} \]

To assess convergence, we need to examine whether the general term tends to zero as \( n \to \infty \). This is a necessary condition for convergence.

So we compute the limit of the general term:

\[ \lim_{n \to \infty} \frac{n}{2n+1} \]

According to the necessary condition for convergence, if the series \( \sum a_n \) converges, then it must be that \( \lim_{n \to \infty} a_n = 0 \). If this limit is not zero, the series diverges automatically.

To evaluate the limit, we divide both the numerator and denominator by \( n \) to simplify the expression:

\[ \lim_{n \to \infty} \frac{1}{2 + \frac{1}{n}} = \frac{1}{2 + 0} = \frac{1}{2} \]

The limit of the general term is not zero, but rather \( \frac{1}{2} \):

\[ \lim_{n \to \infty} a_n = \frac{1}{2} \neq 0 \]

This implies that although the terms are positive, they do not approach zero.

Therefore, the series $ \sum_{n=1}^{\infty} \frac{n}{2n+1} $ is divergent.

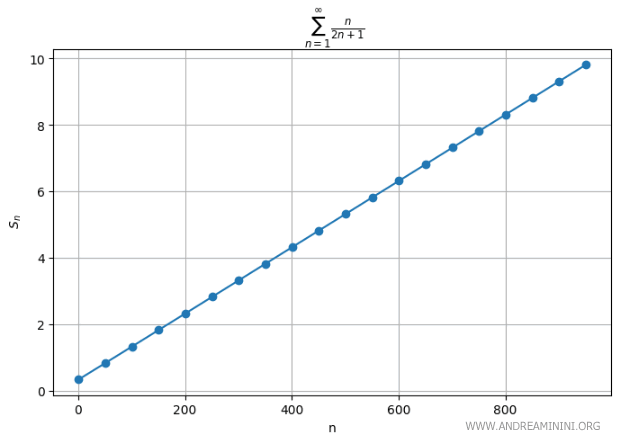
And so on.