Exercise: Analysis of the Numerical Series $ \sum_{n=1}^{\infty} \frac{2^n - 1}{2^n} $

We are tasked with analyzing the behavior of the series:

$$ \sum_{n=1}^{\infty} \frac{2^n - 1}{2^n} $$

The general term of the series is given by:

$$ a_n = \frac{2^n - 1}{2^n} $$

This expression can be simplified as follows:

$$ a_n = \frac{2^n - 1}{2^n} = \frac{2^n}{2^n} - \frac{1}{2^n} = 1 - \frac{1}{2^n} $$

Let’s now evaluate the limit of the sequence \( a_n \) as \( n \) approaches infinity:

$$ \lim_{n \to \infty} a_n $$

$$ \lim_{n \to \infty} \left(1 - \frac{1}{2^n}\right) $$

$$ \lim_{n \to \infty} 1 - \lim_{n \to \infty} \frac{1}{2^n} = 1 - 0 = 1 $$

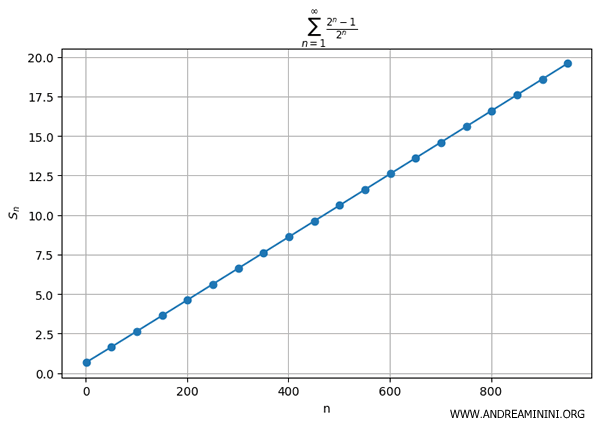
Since the limit of the general term is not zero, the necessary condition for convergence fails. As a result, the series diverges.

Indeed, we can rewrite the original series as the difference of two known series:

$$ \sum_{n=1}^{\infty} a_n = \sum_{n=1}^{\infty} \left(1 - \frac{1}{2^n}\right) = \sum_{n=1}^{\infty} 1 - \sum_{n=1}^{\infty} \frac{1}{2^n} $$

The first series on the right-hand side clearly diverges (being a sum of infinitely many ones), while the second is a convergent geometric series. The divergence of the first term dominates, hence:

The series is divergent.

And so on.