Volume
Volume in physics refers to the amount of space occupied by a body or object.
It’s a fundamental physical quantity measured in cubic meters (m³) in the International System of Units (SI), but it can also be expressed in other units, such as liters (L) for liquids.
In dimensional analysis, volume is described as a derived physical quantity from lengths, so its dimension is represented as:
$$ [V] = [L^3] $$
Here, \( L \) stands for the dimension of length.
This notation shows that volume is the product of three lengths.
For instance, when calculating the volume of a rectangular prism, you multiply its length, width, and height (all measured in units of length) to get a volume in cubic units.
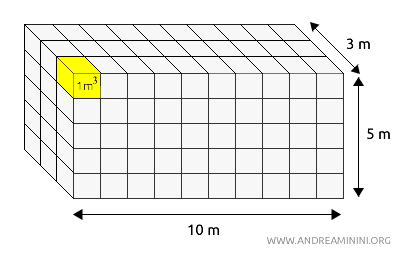
In this case, the rectangular prism has a length of 10 meters, a width of 3 meters, and a height of 5 meters. So, its volume is the product of these three dimensions.
$$ V = 10 \ m \cdot 3 \ m \cdot 5 \ m = (10 \cdot 3 \cdot 5) \ m^3 = 150 \ m^3 $$
Dimensionally, this is written as \( [L^3] \).
This notation is crucial in physics because it helps verify the dimensional consistency of equations before reviewing calculations and helps understand how physical quantities relate to one another.
Volume is essential for determining other physical properties like density, which is the ratio of an object’s mass to its volume (Density = Mass / Volume). It is particularly useful in physics and chemistry when calculating the amount of a substance in a given space, especially for gases and liquids.
Volume formulas
The volume of an object depends on its shape. For example:
- Cube $$ V = l^3 $$ where \( l \) is the length of one side of the cube.
- Rectangular Prism $$ V = l \cdot w \cdot h $$ where \( l \), \( w \), and \( h \) represent the length, width, and height, respectively.
- Sphere $$ V = \frac{4}{3} \pi r^3 $$ where \( r \) is the sphere’s radius.
- Cylinder $$ V = \pi r^2 h $$ where \( r \) is the radius of the base and \( h \) is the height of the cylinder.
- Cone $$ V = \frac{1}{3} \pi r^2 h $$ where \( r \) is the base radius and \( h \) is the height of the cone.
- Pyramid $$ V = \frac{A_{base} \cdot h}{3} $$ where \( A_{base} \) is the base area and \( h \) is the pyramid's height.
Example: If a cube has a side length of 2 meters, its volume is: $$ V = 2^3 = 8 \text{ m}^3 $$ A sphere with a radius of 3 meters will have a volume of: $$ V = \frac{4}{3} \pi (3)^3 \approx 113.1 \text{ m}^3 $$
Multiples and submultiples of volume units
The primary volume unit in the International System of Units (SI) is the cubic meter (\( \text{m}^3 \)), but various multiples and submultiples are used for convenience in different contexts. Here’s a summary:
| Multiple/Submultiple | Symbol | Conversion with \( \text{m}^3 \) |
|---|---|---|
| Cubic Kilometer | \( \text{km}^3 \) | 1 \( \text{km}^3 \) = \( 10^9 \, \text{m}^3 \) |
| Cubic Hectometer | \( \text{hm}^3 \) | 1 \( \text{hm}^3 \) = \( 10^6 \, \text{m}^3 \) |
| Cubic Decameter | \( \text{dam}^3 \) | 1 \( \text{dam}^3 \) = \( 10^3 \, \text{m}^3 \) |
| Cubic Meter | \( \text{m}^3 \) | 1 \( \text{m}^3 \) |
| Cubic Decimeter | \( \text{dm}^3 \) | 1 \( \text{dm}^3 \) = \( 10^{-3} \, \text{m}^3 \) |
| Cubic Centimeter | \( \text{cm}^3 \) | 1 \( \text{cm}^3 \) = \( 10^{-6} \, \text{m}^3 \) |
| Cubic Millimeter | \( \text{mm}^3 \) | 1 \( \text{mm}^3 \) = \( 10^{-9} \, \text{m}^3 \) |
Submultiples are used to measure smaller volumes than the cubic meter. The most common include:
For example, one cubic decimeter (\( \text{dm}^3 \)) equals \( 0.001 \, \text{m}^3 \) and is equivalent to 1 liter (L).
$$ 1 \, \text{dm}^3 = 10^{-3} \, \text{m}^3 $$
One cubic centimeter (\( \text{cm}^3 \)) equals \( 0.000001 \, \text{m}^3 \), which is equivalent to 1 milliliter (mL).
$$ 1 \, \text{cm}^3 = 10^{-6} \, \text{m}^3 $$
Multiples, on the other hand, are used for much larger volumes than the cubic meter. Common examples include:
For instance, one cubic decameter (\( \text{dam}^3 \)) is equivalent to 1,000 cubic meters.
$$ 1 \, \text{dam}^3 = 10^3 \, \text{m}^3 $$
Conversion factors
The conversion factor between different multiples and submultiples of volume follows the cubic principle since volume is a three-dimensional measurement composed of the product of three lengths.
As a result, each unit change involves a factor of \( 10^3 \).
In other words, when converting from a unit of length to a unit of volume, you raise the ratio to the power of three.
For instance, converting from meters to decimeters requires multiplying by \( 10^3 \) because 1 meter equals 10 decimeters in length, width, and depth. Therefore:
$$ 1 \, \text{m}^3 = 10 \ \text{dm} \times 10 \ \text{dm} \times 10 \ \text{dm} = (10 \ \text{dm})^3 = 1,000 \, \text{dm}^3 $$
This rule applies to all volume units, meaning every scale change involves multiplying or dividing by \( 10^3 \). Here’s how it works:
| Conversion Step | Conversion Factor |
|---|---|
| From km³ to hm³ | \( 10^3 \) |
| From hm³ to dam³ | \( 10^3 \) |
| From dam³ to m³ | \( 10^3 \) |
| From m³ to dm³ | \( 10^3 \) |
| From dm³ to cm³ | \( 10^3 \) |
| From cm³ to mm³ | \( 10^3 \) |
For example, to convert 1 cubic meter (\( \text{m}^3 \)) into cubic centimeters (\( \text{cm}^3 \)):
I consider that 1 meter = 100 centimeters.
$$ 1 \, \text{m}^3 = (100 \, \text{cm})^3 = 1,000,000 \, \text{cm}^3 = 10^6 \, \text{cm}^3 $$
This principle applies to all conversions, making volume units easy to scale by following this basic rule.
A more complex conversion example: To convert 7 hm3 (cubic hectometers) to cm3 (cubic centimeters). I write an equation where $ x $ is an unknown variable. $$ 7 \ \text{hm}^3 = x \ \text{cm}^3 $$ I replace the hectometer (hm) with its respective power of ten, 102m, and the centimeter (cm) with 10-2. $$ 7 \cdot (10^2)^3 = x \cdot (10^{-2})^3 $$ I then perform the algebraic calculation between the powers to find x.$$ 7 \cdot 10^6 = x \cdot 10^{-6} $$ $$ x = \frac{ 7 \cdot 10^6}{ 10^{-6}} $$ $$ x = 7 \cdot 10^{6-(-6)}$$ $$ x = 7 \cdot 10^12 $$ I then substitute this value back into the initial equation: $$ 7 \ \text{hm}^3 = x \ \text{cm}^3 $$ $$ 7 \ \text{hm}^3 = 7 \cdot 10^{12} \ \text{cm}^3 $$ This approach converts cubic hectometers to cubic centimeters. This general procedure can be used to switch between multiples and submultiples, but knowledge of algebraic operations with powers is necessary.
Alternatively, I can count the number of decimal point shifts to switch between a multiple and a submultiple (or vice versa), treating each shift as a multiplication or division by a power of 103.
- When converting from a multiple to a submultiple, multiply by 103 for each shift to the right.
- When converting from a submultiple to a multiple, divide by 103 for each shift to the left.
Example: To convert 7 hm3 (cubic hectometers) to cm3 (cubic centimeters). To go from hectometers (hm) to centimeters (cm), I shift the decimal point 4 places to the right.
- From hm (hectometers) to dam (decameters)
- From dam (decameters) to m (meters)
- From m (meters) to dm (decimeters)
- From dm (decimeters) to cm (centimeters)
The liter
Besides the multiples and submultiples of the cubic meter, other common volume units are used. The liter (L) is widely used to measure the volume of liquids.
One liter is equivalent to one cubic decimeter:
$$ 1 \, \text{L} = 1 \, \text{dm}^3 $$
Submultiples like the milliliter (mL) are also used, where:
$$ 1 \, \text{mL} = 1 \, \text{cm}^3 = 0.001 \, \text{L} $$
And so forth.
