The Difference Between Bias and Variance in Machine Learning

In machine learning, bias and variance are two fundamental concepts that significantly influence a model's performance. Striking the right balance between these elements is crucial for developing effective models.

• Bias
  Bias measures the accuracy of a model's predictions on the data it was trained on. If the model makes accurate predictions on this data, it has low bias. Conversely, a model with high bias frequently errs on the training data, indicating poor adaptability.

  This situation, known as underfitting, occurs when the model is overly simplistic or its features are not adequately representative of the data being handled.

• Variance
  Variance focuses on how much a model's predictions vary when applied to different data sets. High variance manifests when a model trained on a specific data set fails to make accurate predictions on new data.

  This phenomenon, called overfitting, results from an overly complex model that fits too tightly to the training data, losing the ability to generalize.

The real dilemma in machine learning is the trade-off between bias and variance. Increasing a model's complexity reduces bias but increases variance, and vice versa.

The ideal model minimizes both bias, to ensure accuracy on the training set, and variance, to guarantee the model's generalizability to new data.

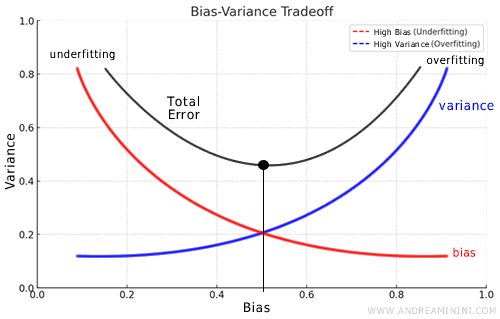
Therefore, balancing bias and variance is essential for optimizing a model's overall performance.

The challenge is to create a model that is neither too simple (risking underfitting) nor overly complex (risking overfitting), but that has the right balance to perform well on both training and new data.

Note. For more on the difference between overfitting and underfitting.

This balance can be achieved through techniques such as regularization and is essential for the development of effective and generalizable machine learning models.

Ideally, a model would minimize both bias and variance, but often this is not possible if the predictive problem is complex.

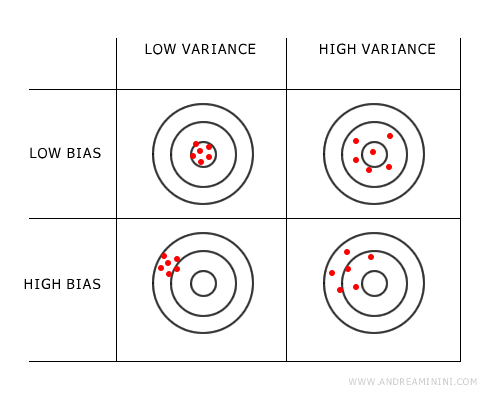
Depending on the problem and the goal, I might choose to minimize bias at the expense of some variance, or vice versa, or find the right equilibrium between the two.

Certainly, there is no one-size-fits-all solution for every situation.

And so on.