Categories (Category Theory)
A category consists of a collection of objects and morphisms.
Objects can be anything, such as sets, groups, or vectors.
Morphisms are the connections between objects, typically represented as arrows flowing from a "domain" object to a "codomain" object. Essentially, morphisms function as mappings between objects.
Consider the category "Set" that includes two sets, A and B: $$ Obj(Set) = \{A, B \} $$ Here, A and B are the objects of the category. $$ A = \{ 2, 3, 5 \} $$ $$ B = \{ 4, 9, 25 \} $$ A possible morphism is the function f(x) = x2, mapping A to B: $$ f: A \rightarrow B $$ Typically, the set of all morphisms in a category is denoted by the symbol $ Mor(Set) $.
Categories also encompass compositions of morphisms and identity morphisms.
- Composition of Morphisms:
When the codomain of a function f aligns with the domain of another function g, you can compose the two. This results in a composite function $ f \circ g $. - Identity Morphism:
Each object in a category is associated with an identity morphism, which connects each element of the object back to itself. This acts as the neutral element within the morphisms.
The composition laws of morphisms within a category must adhere to the associative property.
For example, considering three morphisms: $$ f: A \rightarrow B $$ $$ g: B \rightarrow C $$ $$ h: C \rightarrow D $$ These compositions are equivalent: $$ h \circ ( g \circ f ) = (h \circ g) \circ f $$
A Practical Example
This example constructs a simple "Set" category that includes finite sets, morphisms, a composition of morphisms, and identities.
The objects of this category are finite sets. For example, three sets:
$$ A = \{1, 2\}$$
$$ B = \{a, b, c\} $$
$$ C = \{\alpha, \beta\} $$
The morphisms in this category are all possible functions from one set to another. Here are some function examples:
$$ f: A \rightarrow B $$
$$ f(1) = a; f(2) = b $$
$$ g: B \rightarrow C $$
$$ g(a) = \alpha; g(b) = \beta; g(c) = \alpha $$
Note: Categories are often depicted as diagrams or graphs, where objects (sets) are nodes and functions (morphisms) are arrows linking these nodes. Compositions are visualized as paths within the diagram. Overall, topological diagrams are highly effective for visualizing and grasping intricate relationships.
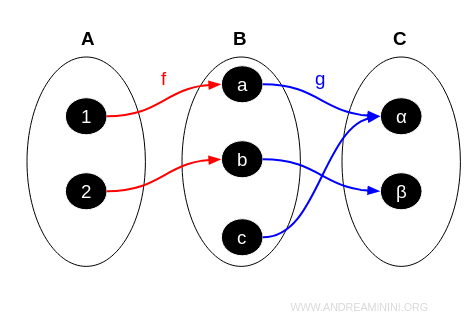
Notice that the morphism \( f: A \rightarrow B \) has a codomain (B) that coincides with the domain of the morphism \( g: B \rightarrow C \). In this scenario, the Set category can also include the composition of the morphisms \( f \) and \( g \).
The composition of morphisms follows the rules of function composition.
$$ g \circ f: A \rightarrow C $$
$$ (g \circ f)(1) = g(f(1)) = \alpha; (g \circ f)(2) = g(f(2)) = \beta $$
In this case, the composition \( g \circ f \) is a function from \( A \) to \( C \), defined by \( (g \circ f)(x) = g(f(x)) \) for each \( x \) in \( A \).
Moreover, every set A, B, C in the category Set has an identity morphism \( \text{id }_X : X \rightarrow X \) mapping each element to itself.
$$ \text{id}_A(1) = 1; \text{id}_A(2) = 2 $$
$$ \text{id}_B(a) = a; \text{id}_B(b) = b; \text{id}_B(c) = c $$
$$ \text{id}_C(\alpha) = \alpha; \text{id}_C(\beta) = beta $$
This example presents a concrete category that is straightforward yet rich enough to illustrate fundamental concepts of category theory.
The structure meets all the requirements of a category: the associativity of compositions and the neutral element provided by the identity for each set.
And so forth.
