Morphisms in Category Theory

In category theory, morphisms serve as connections between objects within a category. $$ f_{AB}: A \rightarrow B $$ Here, A and B are objects, with the arrow symbolizing the morphism. A is the domain and B is the codomain.

Morphisms provide structure and define relationships among objects of the same category, ensuring the preservation of their essential properties.

Each morphism consistently operates from the domain towards the codomain.

For instance, the morphism $ f_{AB} $ maps from object A to object B.

$$ f_{AB}: A \rightarrow B $$

This is in contrast to the morphism $ f_{BA} $, which links the same objects in reverse direction, from B to A.

$$ f_{BA}: B \rightarrow A  $$

Objects in category theory are abstract entities that can vary widely, including sets, groups, vector spaces, matrices, and more.

The collection of all morphisms from one object to another is represented by the symbol hom. For instance, all morphisms from object A to B are grouped under $ hom(A,B) $. The complete set of a category's morphisms is denoted by mor(C), with C being the category’s name.

Morphisms in a category are required to adhere to certain properties:

• Morphism Composition
  Composition involves pairing two morphisms, $ f \in hom(A,B) $ and $ g in hom(B,C) $, where f's codomain is g's domain, resulting in $$ f \circ g \in hom(A,C)$$

  Note: Composition in category theory is associative, meaning if three morphisms are involved, the following relationship holds: $$ f \circ (g \circ h) = (f \circ g) \circ h $$. Typically, the composition of morphisms is non-commutative, meaning $ f \circ g \ne g \circ f $, except in cases involving specific morphisms, such as identity morphisms or in particular categories.

• Identity Morphism
  Each object in a category possesses an identity morphism that links the object back to itself, functioning as the neutral element in composition. $$ 1_A \in hom(A,A) $$ Thus, composing any morphism f with its identity results in f itself: $$ f \circ 1_A = f $$

An Example from Set Theory

Consider the category "Set", which consists of sets.

The objects in this category are sets, with morphisms as functions between these sets.

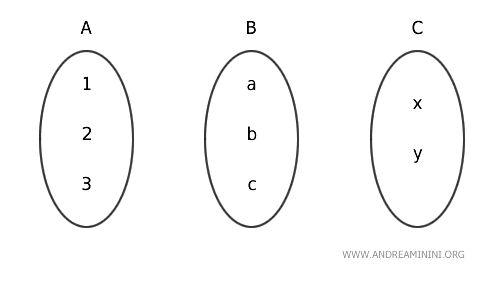
For example, the category includes three distinct sets:

$$ A = \{1, 2, 3\} $$

$$ B = \{a, b, c, d\} $$

$$ C = \{x, y\} $$

A visual representation of these sets is shown below.

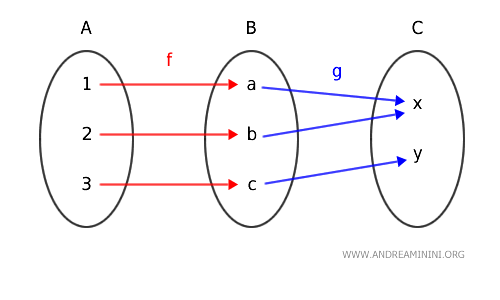
In the "Set" category, two morphisms, f and g, are present:

$$ hom(A,B) = \{ f \} $$

$$ hom(B,C) = \{ g \} $$

Morphism $ f: A \rightarrow B $ simply assigns each element of A to an element of B.

$$ f(1) = a $$

$$ f(2) = b $$

$$ f(3) = c $$

Morphism $ g: B \rightarrow C $ connects the set B to C.

$$ g(a) = x $$

$$ g(b) = x $$

$$ g(c) = y $$

The relationships between morphisms f and g are depicted in the diagram below.

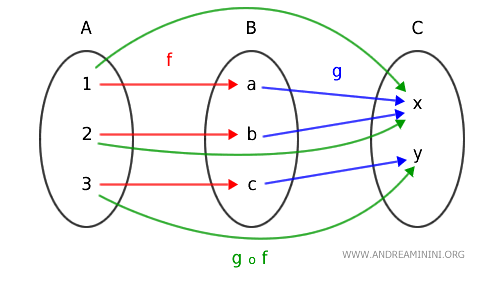
Here, the codomain of morphism f coincides with the domain of morphism g, allowing for their composition:

This results in a new morphism $ g \circ f : A \rightarrow C $

$$ g[f(1)] = g(a) = x $$

$$ g[f(2)] = g(b) = x $$

$$ g[f(3)] = g(c) = y $$ 

Such composition introduces another morphism connecting objects A and C within the "Set" category.

$$ hom(A,C) = \{ g \circ f \} $$

Moreover, each set in the category features an identity morphism that maps each element to itself.

$$ 1_A: A \rightarrow A $$

$$ 1_B: B \rightarrow B $$

$$ 1_C: C \rightarrow C $$

The identity morphism $ 1_A $ connects each element of set A to itself. $$ 1_A(1)=1 $$ $$ 1_A(2)=2 $$ $$ 1_A(3)=3 $$ Similarly, the identity morphism $ 1_B $ links each element of set B to itself $$ 1_B(a)=a $$ $$ 1_B(b)=b $$ $$ 1_B(c)=c $$ Lastly, the morphism $ 1_C $ connects each element of set C to itself $$ 1_C(x) = x $$ $$ 1_C(y) = y $$

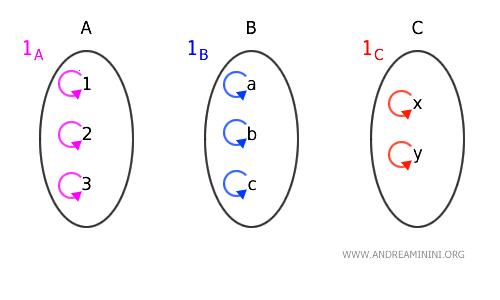
In summary, the set of all morphisms within the Set category includes the direct morphisms $ f, g $, their composition $ g \circ f $, and the identity morphisms $ 1_A, 1_B, 1_C $

$$ Mor(Set) = \{ f, g, g \circ f, 1_A, 1_B, 1_C \} $$

This example should elucidate the concept of morphisms in the set category.

Observations

Some personal thoughts and notes on morphisms in category theory.

• Why do we talk about morphisms instead of relations or functions in category theory?
  In category theory, the term "morphism" is used for several reasons that highlight the abstraction and generality of this branch of mathematics. This term emphasizes a more flexible, abstract, and structural approach to describing mathematical relationships, going beyond the limitations of the traditional definitions of functions and relations. By using "morphism," mathematicians can avoid the specific connotations of terms like "relation" or "function," which usually imply direct and well-defined mappings between individual elements of sets. Morphisms allow for the consideration of more complex and less direct mappings, including structural changes or transformations that are not limited to point-to-point correspondences.

  For example, morphisms generalize the concept of functions and mappings between objects. While a traditional function describes a specific relationship between elements of two sets, a morphism in category theory can describe much more abstract and general operations. This enables the inclusion of various mathematical structures, such as sets, spaces, groups, rings, and more, each with its own "functions" or "transformations" that preserve the internal structure of the objects.

  Additionally, in category theory, objects and morphisms form a structure called a "category," and each category has specific rules on how morphisms can be composed and how they relate to objects. Thus, using the term "morphism" instead of "function" underscores the importance of structural properties (such as composition and identity) that must be satisfied.

  Example: In category theory, a 2x3 matrix can be considered a morphism, but not necessarily in the direct sense of a traditional "relation" or "function" between sets of numbers. A 2x3 matrix has two rows and three columns, so it can transform a vector in 3-dimensional vector space (R³) into a vector in 2-dimensional vector space (R²). $$ f: R^3 \rightarrow R^2 $$ However, this "transformation" does not imply any relationship between the numbers 2 and 3, so it cannot be defined as a "function" between the two numbers. It is more appropriately called a morphism. For further details, see this example.

And so forth