The Category of Posets in Category Theory

In the category of posets (partially ordered sets), there can be at most one direct morphism $a \rightarrow b$ between any pair of objects $a, b$ within set P. Morphisms in this context are defined as order relations.

Typically, a poset is a set $P$ with an order relation $\leq$ that is reflexive, antisymmetric, and transitive.

$$ Poset (P, \leq) $$

This implies that within the set:

each element is equivalent to itself $ a = a $ (reflexivity),
if $a \leq b$ and $b \leq a$, then $a = b$ (antisymmetry),
if $a \leq b$ and $b \leq c$, then $a \leq c$ (transitivity).

These properties qualify posets as a category ($P, \leq$) with specific structures:

Objects: The elements of the set $P$.
Morphisms: Functions between two objects $a, b \in P$ that exist only if $a \leq b$. There is a unique morphism for each pair $a \leq b$, representing the order relation between $a$ and $b$. All order relations adhere to associativity.
Note: Like other categories, all morphisms between two objects are part of the hom-set(a, b). Generally, all morphisms in set $P$ are part of the set $Mor(P)$.
Morphism Composition: If there are morphisms from $a$ to $b$ and from $b$ to $c$, reflecting $a \leq b$ and $b \leq c$, a direct and unique morphism from $a$ to $c$ must exist due to the transitivity of the order.
Identity Morphism: Each element $a \in P$ inherently possesses an identity morphism due to the reflexive nature of the order relation.

Thus, a poset meets all the criteria of a category.

In essence, category theory applied to posets provides a structured and abstract framework for analyzing order relations within partially ordered sets.

An Illustrative Example

Each natural number $n \in \mathbb{N}$ can be considered a set that includes all natural numbers less than $n$, from $0$ to $n-1$.

$$ \mathbb{N} = \{ 0,1,2,3,4,5,... \} $$

The natural number $0$ is defined as the empty set $\emptyset$ since it lacks predecessors.

$$ 0 = \{ \} $$

Conversely, the natural number $1$ is a singleton set, having only $0$ as its predecessor.

$$ 1 = \{ 0 \} $$

Following this pattern, the natural number $2$ is defined by its predecessors $0$ and $1$.

$$ 2 = \{ 0,1 \} $$

This structure implies that each natural number inherently forms a category where the objects are the numbers less than itself, and the morphisms reflect the natural or inclusion relations among these numbers.

For example, consider the natural number $3$ as a category.

The category of number 3 consists of all natural numbers preceding it:

$$ 3 = \{0, 1, 2\} $$

Here, the objects are the numbers $0$, $1$, and $2$.

The morphisms are established through the natural order ($\leq$), where a morphism exists from one number to another if the former is less than or equal to the latter.

The morphisms in this category include:

$$ id_0: 0 \rightarrow 0 $$

$$ id_1: 1 \rightarrow 1 $$

$$ id_2: 2 \rightarrow 2 $$

$$ f: 0 \rightarrow 1 $$

$$ g: 0 \rightarrow 2 $$

$$ h: 1 \rightarrow 2 $$

The first three morphisms are identity morphisms, as each element relates to itself in the order $ \leq $. The other morphisms represent ascending order relations among different objects: $ 0 \leq 1 $, $ 0 \leq 2 $, and $ 1 \leq 2 $.

The respective hom-sets are as follows:

hom(0, 0): Contains only the identity of $0$, $\text{id}_0$.
hom(1, 1): Contains only the identity of $1$, $\text{id}_1$.
hom(2, 2): Contains only the identity of $2$, $\text{id}_2$.
hom(0, 1): Contains the morphism $f$, representing $0 \leq 1$.
hom(0, 2): Contains the morphism $g$, representing $0 \leq 2$.
hom(1, 2): Contains the morphism $h$, representing $1 \leq 2$.

Note: The hom-sets hom(1, 0), hom(2, 0), and hom(2, 1) are empty because no order relations descend from a larger to a smaller number.

The morphism $f$ composed with $h$ results in $g$, demonstrating the transitivity of the natural order.

$$ h \circ f = g $$

Graphically, this category can be depicted as follows:

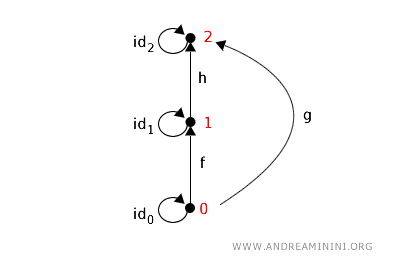
category diagram

This diagram uses arrows to indicate morphisms, showing an ascending order relation.

The set of all morphisms in this category includes six morphisms:

$$ Mor(3) = \{ id_0, id_1, id_2, f, g, h \} $$

In summary, this example illustrates how a set of natural numbers less than a given number can be organized into a category, with objects and morphisms reflecting the natural order relations. Here, the numbers themselves serve as objects, and their relational orderings as morphisms.