The Groupoid Category

A groupoid category is defined as a category in which every morphism is an isomorphism, meaning that each morphism is reversible. This structure mirrors the properties of an equivalence relation.

In a groupoid category, since each morphism is an isomorphism, each morphism has an inverse.

This characteristic ensures that all relationships between objects in the category embody an equivalence relation, adhering to the following properties:

• Reflexivity: Every object possesses an identity morphism that maps it to itself.
• Symmetry: For each morphism that maps object \(a\) to \(b\), there exists an inverse morphism that maps \(b\) back to \(a\).
• Transitivity: If there is a morphism from \(a\) to \(b\) and another from \(b\) to \(c\), a composite morphism from \(a\) to \(c\) is also available.

Thus, in a groupoid, every object is reflexively related to itself through its identity, symmetrically connected through its inverse, and the composition of morphisms ensures transitivity.

In a groupoid, it is also possible for multiple morphisms to exist between two objects, provided each morphism can be reversed.

Unlike in the preorder category or the poset category, a groupoid category does not limit the number of morphisms between two objects. What characterizes a groupoid is not the uniqueness of the morphisms between objects but rather that every morphism is an isomorphism, each with its own inverse.

A Practical Example

Consider the groupoid of symmetries for a geometric object, such as a square.

In this groupoid category:

• The objects are points on the square,
• The morphisms are transformations that shift one point to another while maintaining the square’s integrity. These transformations include 90, 180, and 270-degree rotations, and reflections across axes.

In this category, each morphism is paired with an inverse.

For instance, a 90-degree clockwise rotation is countered by a 270-degree clockwise rotation (or 90 degrees counterclockwise).

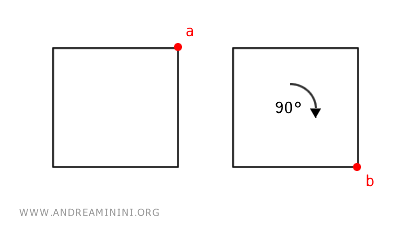
Additionally, the same morphism between any two points \(a\) and \(b\) can be achieved by rotating 360° plus 90°. The outcome is identical to a simple 90° rotation, and so on.

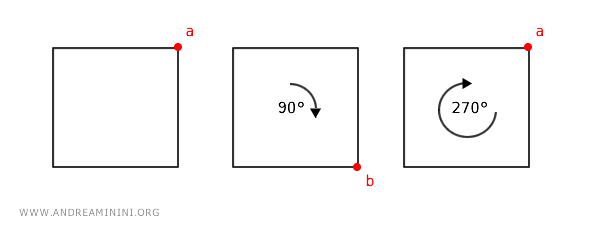
The essential feature here is that every transformation is reversible, offering multiple ways to change one point to another through various combinations of rotations and reflections.

This example illustrates that in a groupoid category, unlike in a poset, there can indeed be more than one morphism between two objects, as long as each morphism can be nullified by another.