Preordered Categories in Category Theory

A preordered category is a type of category characterized by having at most one direct morphism between each pair of objects, where these morphisms function as preorder relations.

Preordered categories adhere to two fundamental morphism properties:

• Reflexivity: Every object relates to itself.
• Transitivity: If an object A is related to object B, and B is related to object C, then A must relate to C.

When a morphism exists from A to B, we describe A as less than or equal to B, denoted A ≤ B.

Essentially, a preordered category can be viewed as a structured ordering of objects, dictated by the existence of morphisms among them.

Note: The symbol ≤ generally indicates a preorder relation between objects. It could represent the traditional greater-than-or-equal-to operator, or even set inclusion, among other relationships.

A Practical Example

Consider the following set of objects:

$$ S = (A, B, C, D) $$

I then define morphisms between these objects:

$$ A \rightarrow A $$

$$ B \rightarrow B $$

$$ C \rightarrow C $$

$$ A \rightarrow B $$

$$ A \rightarrow C $$

$$ B \rightarrow D $$

$$ C \rightarrow D $$

$$ B \rightarrow C $$

$$ C \rightarrow B $$

These objects and morphisms are illustrated in the following diagram:

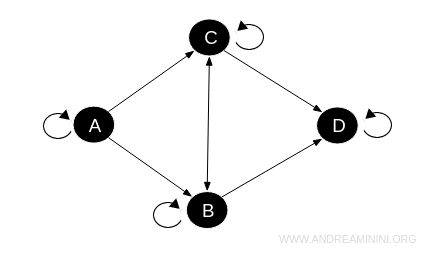
The morphisms in this category demonstrate:

• Reflexivity: Each object is inherently related to itself through identity morphisms.
• Transitivity: For instance, if \(A \rightarrow B\) and \(B \rightarrow D\), then necessarily \(A \rightarrow D\), and so on.

Unlike a poset category, a preordered category does not require antisymmetry.

For example, the relationship between \(B\) and \(C\) is bidirectional, as represented by \(B \rightarrow C\) and \(C \rightarrow B\).

What is the antisymmetry property? Antisymmetry means that if two distinct objects are reciprocally related, they must actually be the same object. This property is not mandatory in preordered categories, allowing for two objects to be reciprocally related yet remain distinct or considered "equivalent".

Thus, the structure and relationships define a preordered category.

Comparing Preordered and Poset Categories

The key difference between preordered and poset categories lies in the antisymmetry property:

• Preordered Category
  Here, each pair of objects has at most one morphism. These morphisms satisfy reflexivity and transitivity but not necessarily antisymmetry. Reciprocal morphisms between two objects \( A \) and \( B \) (from \( A \) to \( B \) and vice versa) do not imply they are the same object; they may be distinct yet regarded as equivalent.
  
• Poset Category
  In poset categories, morphisms are strictly order relations, adhering to reflexivity, transitivity, and antisymmetry. If reciprocal morphisms exist between two objects \( A \) and \( B \), they must be identical. Here, too, only one direct morphism is allowed between any two objects.
  

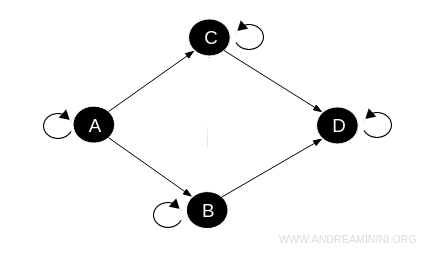
Ultimately, the decision to use a preordered or poset category depends on whether to treat equivalences between objects as identical or merely functionally similar.

And so on.