Category Theory

Category theory is a branch of mathematics that delves into abstract structures and their interactions. It fundamentally comprises "objects" and "morphisms" (also referred to as arrows) that connect these objects.

Morphisms in this field abstract the concept of functions between mathematical structures.

Categories represent a third level of abstraction, building upon individual set elements and the structures defined on those sets, such as groups, rings, fields, vector spaces, and so on.

Purpose

Category theory serves to unify various mathematical concepts under a high-level abstract framework. It applies across multiple disciplines including mathematics, physics, and computer science, facilitating a broader understanding of complex relationships.

Essentially, it enables the transfer of insights and methodologies from one structure to another, revealing universal structural properties that transcend the specific details of the involved structures.

This capability allows an idea conceived in one context to be adapted and applied to solve problems in completely different contexts.

Example. The Dijkstra's algorithm was initially designed to identify the shortest path in computer networks. When viewed more abstractly, this algorithm determines the shortest path from a starting node to all other nodes in a weighted graph.

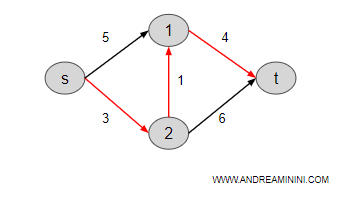
Today, the applications of this algorithm extend well beyond its computational origins. In logistics, it optimizes delivery routes to minimize travel time or distance. It enhances public transportation planning by identifying the most efficient routes across a city. In computational biology, it is used to analyze protein interaction networks, pinpointing key signaling pathways. It even plays a role in the analysis of economic or financial networks, where it helps streamline the flow of capital or information. The foundational principles of Dijkstra's algorithm have thus found diverse applications across various fields.

The aim of category theory is to discern the abstract structure underlying different mathematical and scientific areas, thereby enabling the exploration and understanding of object and morphism interactions on a universal scale, independent of specific disciplinary details.

By facilitating the cross-disciplinary transfer of methods and results, it reveals shared properties and offers fresh insights through a standardized and formal language.

Components of Category Theory

The core elements of category theory include:

• Categories
  A category is a collection of "objects" interconnected by "morphisms," which serve as bridges between these objects, adhering to strict composition rules.

  Example. A quintessential example of a category is the category of sets, known as Set. Here, objects are all conceivable sets, and morphisms are all possible functions between these sets, with morphism composition mirroring the traditional function composition.

• Objects
  Objects can be anything from simple sets to complex structures like rings or vector spaces. They are the fundamental nodes where morphisms initiate or conclude.

  Example. Groups are the objects of the category of Groups, commonly referred to as Grp. In this category, the objects are groups, and the morphisms are group homomorphisms, which are functions that preserve the group operation. These morphisms are composed in the same way as functions, ensuring that the group's structural properties are maintained.

• Morphisms
  Morphisms are the connections or functions between objects, each with a specified origin and destination. Their compositions must be associative, and each object must have an identity morphism, which acts as a neutral element in their composition.

  Example. An example of a morphism is a group homomorphism, such as the function \( f: \mathbb{Z} \rightarrow \mathbb{Z}_6 \) defined by \( f(x) = x \mod 6 \). This morphism honors the addition operation of integers, ensuring that the sum of two elements in the domain maps to their summed counterparts in the codomain modulo 6, within modular arithmetic.

• Composition of morphisms
  Morphism composition is a key operation in category theory. If \( f \) is a morphism from \( A \) to \( B \), and \( g \) is from \( B \) to \( C \), then a composite morphism \( g \circ f \) exists from \( A \) to \( C \).

  Example. Consider two functions: \( f: \mathbb{R} \to \mathbb{R} \) defined by \( f(x) = x+1 \) and \( g: \mathbb{R} \to \mathbb{R\) defined by \( g(x) = 2x \). The composition \( g \circ f \) results in a new function from \( \mathbb{R} \) to \( \mathbb{R \) that applies \( f \) first, then \( g \). The final result, \( g[f(x)] = 2(x+1) = 2x + 2 \), is a practical demonstration of the composite function concept.

• Identity
  Every object in a category possesses an identity morphism, which serves as a neutral element for composition. This ensures that any morphism composed with the identity results in the original morphism.

  Example. The set of real numbers \( \mathbb{R} \) serves as an object with the identity morphism \( \text{id}_{\mathbb{R}}: \mathbb{R} \to \mathbb{R} \) defined as \( \text{id}_{\mathbb{R}}(x) = x \), which leaves every element of the domain unchanged. This function plays a crucial role in maintaining the integrity of any morphism composed with it.

In mathematics, exploring relationships between various structures through connecting functions, known as morphisms, is highly beneficial.

This method emphasizes general properties and relationships over the individual elements (objects) within the structures, offering a more unified and adaptable view of mathematics.

As a result, mathematical structures are characterized by their transformations into one another, rather than by their standalone features.

The History of Category Theory

Introduced in the 1940s by mathematicians Samuel Eilenberg and Saunders Mac Lane, category theory was initially devised to formalize and analyze complex structures in algebraic topology, especially in relation to natural transformations and functors.

Since its inception, category theory has broadened its influence significantly, impacting numerous fields within pure and applied mathematics.

Its capacity to uncover profound structural connections across diverse mathematical domains has introduced novel insights and methodologies in fields ranging from algebra and logic to set theory and theoretical computer science, as well as theoretical physics.

With developments in the 1960s and '70s, such as monoidal categories, higher categories, and toposes, category theory continued to evolve, offering new tools and perspectives.

Today, it remains a dynamic field of study, proving its enduring value as a universal language in mathematics.