The Category of Matrices Over a Finite Field

The category Matr(F) is a mathematical framework where objects are positive integers m,n∈Z⁺, and morphisms are m×n matrices with elements from the finite algebraic field F. This field is often denoted as F_p to emphasize its finite nature, where p is a prime number.

For example, F₃ is a finite field with three elements {0,1,2}, where all arithmetic operations are carried out modulo 3. Here, the matrix elements are limited to 0, 1, or 2.

Here’s a closer look at this category:

• Objects
  The objects in the category Matr(F) are represented by positive integers $ m,n \in \mathbb{Z} $, indicating the dimensions of matrices constructed from elements of the field \( F \). Hence, the integers define the matrix dimensions rather than the matrices themselves.
• Morphisms
  Morphisms between two objects \( m \) and \( n \) are all matrices of dimension \( m \times n \) with elements from \( F \). These morphisms facilitate linear transformations from a vector space of dimension \( n \) to one of dimension \( m \), both defined over \( F \). For m=n, the morphism is a square matrix nxn; if m≠n, it’s a rectangular matrix mxn.
• Composition of Morphisms
  Morphism composition in Matr(F) adheres to the standard rules of matrix multiplication. If \( A \) is a matrix \( m \times n \) and \( B \) is a matrix \( n \times s \), the resulting product matrix \( AB \) is \( m \times s \), achieved by multiplying \( A \) with \( B \). $$ AB = A \times B $$

  Note: Not all morphisms can define a composition, as matrix multiplication between two matrices M1×M2 is feasible only if the number of columns in M1(m,n) matches the number of rows in M2(n,s).

• Identity
  Each object \( n \) possesses an identity morphism, which is the identity matrix \( I_n \), a square matrix \( n \times n \) with 1s along its diagonal and 0s elsewhere. This matrix serves as the neutral element in compositions with other square matrices \( n \times n \). However, rectangular matrices \( m \times n \) with m≠n lack an identity morphism.

The category Matr(F) proves invaluable for studying and handling linear transformations within a stringent algebraic framework.

Viewing matrices as morphisms enables a deeper exploration of linear algebra concepts involving the manipulation of vector spaces and linear transformations in an abstract and sophisticated manner.

A Practical Example

Consider the category Matr(F₃), which encompasses objects, morphisms, morphism composition, and the identity element, utilizing the finite field \(\mathbb{F}_3\) with elements {0, 1, 2}, and operations performed modulo 3.

For instance, 1+1=2 because 2 modulo 3 is equal to 2, since 2 divided by 3 yields a quotient of zero with a remainder of 2. Conversely, 1+2=0 because 3 modulo 3 is zero, with 3 divided by 3 yielding a quotient of one and a remainder of zero. Essentially, modular arithmetic involves stating the remainder. Below are the general additive and multiplicative tables for operations modulo 3.

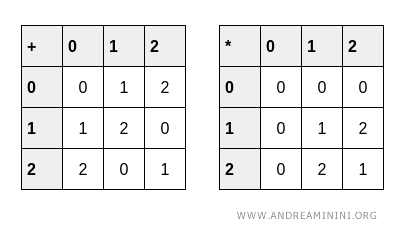
The category includes the following objects and morphisms:

• Objects in Matr(\(\mathbb{F}_3\))
  Objects within Matr(\(\mathbb{F}_3\)) are all positive integers $ m,n \in \mathbb{Z} $, specifying matrix dimensions in terms of rows and columns.
• Morphisms
  Morphisms between category objects are matrices $ m \times n $ with elements from F ₃ equal to 0, 1, or 2. Thus, every morphism from object $ m $ to object $ n $ represents all matrices \( m \times n \). If m≠n, these matrices are rectangular; if m=n, they are square.

  For example, the morphism from object 2 to object 3 represents all \( 2 \times 3 \) matrices like the following $$ A = \begin{bmatrix}
  1 & 2 & 0 \\
  2 & 0 & 1
  \end{bmatrix}
  $$ Likewise, the morphism from object 3 to object 2 includes all \( 3 \times 2 \) matrices such as $$
  B = \begin{bmatrix}
  0 & 1 \\
  1 & 0 \\
  2 & 2
  \end{bmatrix} $$ Here, all matrices contain elements solely from F₃, with possible dimensions ranging from 1x1 up to 100x100, as defined by the positive integers m,n∈Z⁺.

• Composition of Morphisms
  The composition of morphisms relies on matrix multiplication.

  As an example, composing a 3×2 matrix with a 2×3 matrix produces: $$ BA = \begin{bmatrix} 0 & 1 \\
  1 & 0 \\
  2 & 2
  \end{bmatrix} \begin{bmatrix}
  1 & 2 & 0 \\
  2 & 0 & 1
  \end{bmatrix} = \begin{bmatrix}
  2 & 0 & 1 \\
  1 & 2 & 0 \\
  0 & 2 & 2
  \end{bmatrix} $$ Operations between matrix elements are calculated modulo 3. For instance, multiplying 2 by 2 yields 4, but 4 divided by 3 results in 1 with a remainder of 1, hence 2x2 equals 1 modulo 3.

• Identity Element
  Each object \( n \) is associated with an identity morphism, which is an identity matrix \( n \times n \): - The identity for object 1 is \( \begin{bmatrix} 1 \end{bmatrix} \).
  - The identity for object 2 is \( \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \).

  For instance, multiplying a 2×2 matrix A by the identity matrix I₂ consistently yields the original matrix A: $$ AI_2 = \begin{bmatrix} 1 & 2 \\ 2 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 2 & 0 \end{bmatrix} $$ This rule applies across all dimensions, linking each square matrix of size $ n \times n $ to its corresponding identity matrix $ I_n $.

Through this framework, Matr(F₃) thoroughly addresses linear transformations and algebraic operations in a discrete setting.

One of the practical applications of this category is in cryptography.

This setup could be employed in a cryptographic algorithm, an information encoding process, or another application of linear algebra.

And so on.