Functors in Category Theory

In category theory, a functor F maps objects and morphisms between two different categories while preserving their internal structure. $$ F: \text{Obj}(Cat_1 ) \rightarrow \text{Obj}(Cat_2) $$ $$ F: \text{Mor}(Cat_1 ) \rightarrow \text{Mor}(Cat_2) $$

The categories are collections of objects and morphisms (or arrows) between these objects. 

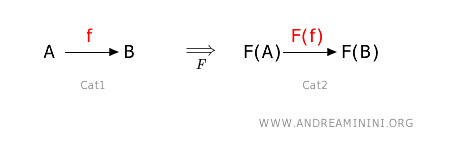
A functor F maps each object in one category to an object in another category and each morphism (arrow) in one category to a morphism in another category.

$$ F: \text{Obj}(Cat_1 ) \rightarrow \text{Obj}(Cat_2) $$

$$ F: \text{Mor}(Cat_1 ) \rightarrow \text{Mor}(Cat_2) $$

Here, Obj(Cat₁) and Obj(Cat₂) represent the sets of objects in categories Cat₁ and Cat₂, respectively, and Mor(Cat₁) and Mor(Cat₂) represent the sets of morphisms in the two categories.

For example, if the morphism $ f: A \rightarrow B $ maps objects A and B in category 1 to objects F(A) and F(B) in category 2, then the morphism $ F(f) : F(A) \rightarrow F(B) $ obtained through the functor F maps the images F(A) and F(B) in category 2.

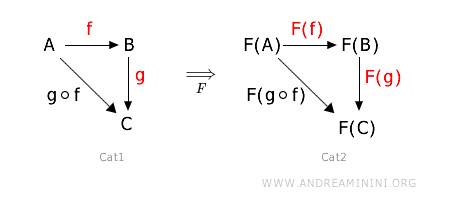
It's crucial that this mapping respects the composition of morphisms.

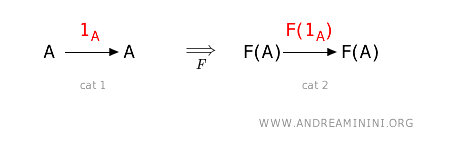
Additionally, it must also respect the identity morphism of objects.

This means that the image of a morphism that composes two other morphisms must be the morphism that is the composition of the images of those two morphisms.

Therefore, the functor preserves the "shape" of the relationships between objects in the source category within the target category.

Note: Functors are useful for transferring problems and solutions between different categories. This allows methods and insights from one context to be applied to another in a consistent and structured way.

Covariance and Contravariance

A functor connects the morphisms between two categories.

$$ F: \text{Mor}(Cat_1 ) \rightarrow \text{Mor}(Cat_2) $$

However, this connection between morphisms can occur in two distinct ways. Functors can be covariant or contravariant.

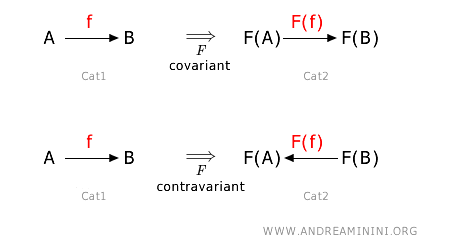
For covariant functors, the direction of the morphisms is preserved, whereas for contravariant functors, it is reversed.

• Covariant
   A covariant functor preserves the direction of the morphisms. If a morphism goes from A to B in the source category, then the corresponding morphism goes from F(A) to F(B) in the target category. $$ F: \text{hom}_{Cat1}(A,B) \rightarrow \text{hom}_{Cat2}(FA,FB) $$ Where hom(A,B) is the set of morphisms from object A to object B. So, for every object A and B in category 1, if $f: A \rightarrow B $ is a morphism in category 1, then $ F(f): F(A) \rightarrow F(B)  $ is the corresponding morphism in category 2. $$f: A \rightarrow B \ \ \  \underset{F}{ \Longrightarrow} \ \ \ F(f): F(A) \rightarrow F(B)  $$
  

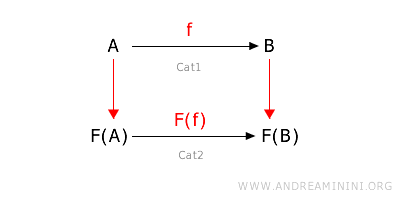
  Note: Covariant functors are natural in many transformations where you want to "follow the direction" of the original functions, such as geometric transformations or operations on data structures.

• Contravariant
  A contravariant functor reverses the direction of the morphisms. If a morphism goes from A to B in the source category, then the corresponding morphism goes from F(B) to F(A) in the target category. $$ F: \text{hom}_{Cat1}(A,B) \rightarrow \text{hom}_{Cat2}(FB,FA) $$ Therefore, for every object A and B in category 1, if $f: A \rightarrow B $ is a morphism in category 1, then $ F(f): F(B) \rightarrow F(A)  $ is the corresponding morphism in category 2. $$f: A \rightarrow B \ \ \  \underset{F}{ \Longrightarrow} \ \ \ F(f): F(B) \rightarrow F(A)  $$  Note that the direction is reversed compared to covariant functors. In this case, it goes from B to A, whereas in covariant functors, it was always from A to B.
   

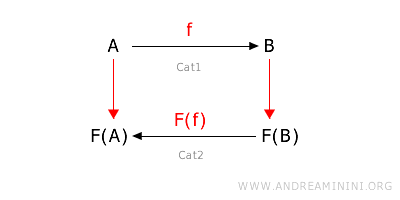
  Note: Contravariant functors are crucial when operations or relationships need to be "reversed," considering pre-images rather than images.

A Practical Example

For example, consider two categories: the category of sets and the category of lists.

These two categories can be connected via a functor that transforms each set into a list.

Let's define the functor "List."

• Objects: For each set \( A \) in the category of sets, the "List" functor associates the list of all elements of \( A \) in the category of lists.

  For example, if \( A \) is the set \( \{1, 2, 3\} \), then \( F(A) \) could be the list [1, 2, 3].

• Morphisms: Every function \( f: A \to B \) between sets is mapped to a function \( F(f): F(A) \to F(B) \) between lists, where \( F(f) \) applies \( f \) to each element of the list.

  For instance, if \( f(x) = x + 1 \) and \( A \) is \( \{1, 2, 3\} \), then \( F(f) \) applied to [1, 2, 3] will produce [2, 3, 4].

The "List" functor preserves the internal structure of the categories. Specifically:

• Preserves compositions in categories
  If there are two functions/morphisms \( f: A \to B \) and \( g: B \to C \) in a category, then the "List" functor preserves the composition even among the lists \( F(g \circ f) = F(g) \circ F(f) \).
• Preserves identity
  The identity function on a set \( A \) is mapped to the identity function on the list \( F(A) \).

  For example, if \( \text{id}_A \) is the identity function on \( A = \{1,2,3 \} \), then \( F(\text{id}_A) \) is the identity function on [1, 2, 3], which leaves every element unchanged.

The "List" functor transforms every operation on single elements into an operation on a more complex data structure like a list.

Note. This type of functor is common in functional programming languages, where data structures and functions can be manipulated in very general and powerful ways.

Example 2

In this example, let's analyze a functor that maps the category of sets to the category of power sets.

1. Category of Sets
   This is the category where the objects are sets and the morphisms are functions between these sets.
2. Category of Power Sets
   This is the category where each object is the power set of a set, meaning the set of all subsets of that set, and the morphisms are functions between these power sets.

We define a functor `P` that maps each set to its power set:

This type of functor transforms sets into power sets and functions into functions between power sets.

• Objects: For each set \( A \), \( P(A) \) is the power set of \( A \).

  For example, if \( A \) is the set \( \{1, 2\} \), then its power set \( P(A) \) will be \( \{\{\}, \{1\}, \{2\}, \{1, 2\}\} \).

• Morphisms: Each function \( f: A \to B \) is transformed into a function \( P(f): P(A) \to P(B) \) that maps each subset of \( A \) to the subset of \( B \) obtained by applying \( f \) to each element of the subset.

  For instance, if \( f(x) = x + 1 \) and \( A \) is \(\{1, 2\}\), then:
  \( P(f)(\{\}) = \{\} \)
  \( P(f)(\{1\}) = \{2\} \)
  \( P(f)(\{2\}) = \{3\} \)
  \( P(f)(\{1, 2\}) = \{2, 3\} \)

As usual, the functor preserves the internal structure of the categories:

• Composition of morphisms: If there are two morphisms \( f: A \to B \) and \( g: B \to C \), then the composition of morphisms is \( P(g \circ f) = P(g) \circ P(f) \).

  This means that applying \( g \) after \( f \) to each element of a subset of \( A \) is equivalent to first applying \( P(f) \) and then \( P(g) \) to the result.

• Identity morphism: If \( \text{id}_A \) is the identity morphism on \( A \), then \( P(\text{id}_A) \) is the identity morphism on \( P(A) \).

Now let's also introduce the concepts of covariant and contravariant functors.

In the category of sets, suppose there is a morphism \( f: A \to A \) defined as \( f(x) = 3 - x \)

For example, if I consider the set \( A = \{1, 2\} \), the morphism connects each object to another. In this case, \( f(1) = 2 \) and \( f(2) = 1 \).

The covariant functor 'P' maps the objects and morphisms of the set to the corresponding power set.

• Objects: It maps \( A \) to \( P(A) \), where \( P(A) = \{\{\}, \{1\}, \{2\}, \{1, 2\}\} \).
• Morphisms: \( P(f): P(A) \to P(A) \), defined by \( P(f)(S) = \{f(x) | x \in S\} \).

Here are some examples of mappings obtained with P(f)

\( P(f)(\{ \}) = \{ \} \)
\( P(f)(\{1\}) = \{2\} \)
\( P(f)(\{2\}) = \{1\} \)
\( P(f)(\{1, 2\}) = \{2, 1\} = \{1, 2\} \)

Thus, the covariant functor `P` preserves the structure of operations by applying the function \( f \) to each element of the set. This reflects the mapping of the element in the original set to the element in the destination set.

The contravariant functor `Q`, on the other hand, maps each set to its power set but reverses the direction of functions.

• Morphisms: \( Q(f): Q(A) \to Q(A) \) is defined by \( Q(f)(T) = \{x | f(x) \in T\} \).

Here are some examples of mappings by Q(f)

\( Q(f)(\{\}) = \{\} \) (no element is mapped to $ \{ \} $)
\( Q(f)(\{1\}) = \{2\} \) (only 2 is mapped to 1 by \( f \))
\( Q(f)(\{2\}) = \{1\} \) (only 1 is mapped to 2 by \( f \))
\( Q(f)(\{1, 2\}) = \{1, 2\} \) (both elements are mapped to \{1, 2\} by \( f \))

The contravariant functor `Q` reverses the direction of the function, considering the pre-image of the elements with respect to the original function.

This shows how the original elements contribute to the formation of the subset in the destination set.

In this example, `P` (covariant) directly applies the function to the elements of the set, while `Q` (contravariant) considers how the elements of the destination set were obtained from the elements of the original set, performing a reverse mapping with respect to the given function.

These examples illustrate how functors can be used to transform and transfer structures between categories in ways that either preserve or invert the direction of the original operations.

I hope this example clarifies the concept of a functor.

And so on.