Theorem of Chords Equidistant from the Center
In a circle, two congruent chords are equally distant from the center - and conversely, two chords that are equally distant from the center are congruent.
This means the converse is also true: two chords equidistant from the center must be congruent.
Proof
The proof can be divided into two parts.
A] Two chords equidistant from the center are congruent
We aim to prove that two chords equidistant from the center O of the circle are congruent.
Consider a circle and two chords AB and CD that lie at the same distance from the center O.
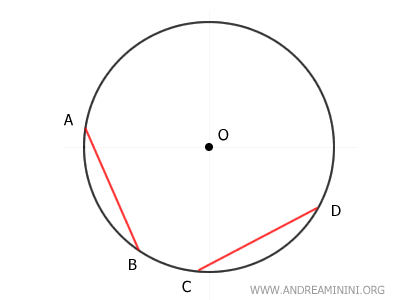
Draw perpendicular segments from O to each chord to represent their distances from the center.
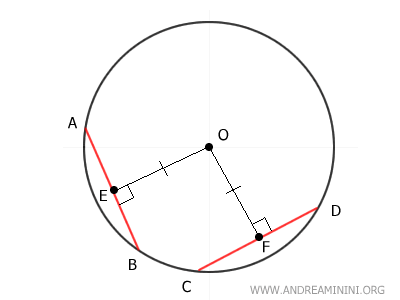
Note. The distance is measured by a segment drawn perpendicularly from the center O to chord AB (or CD).
By our initial assumption, these distances are equal:
$$ \overline{OE} \cong \overline{OF} $$
Now draw segments OB and OD. Since both are radii of the circle, they are congruent:
$$ \overline{OB} \cong \overline{OD} $$
This construction produces two right triangles, OBE and ODF.
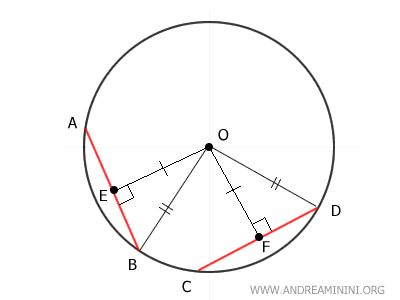
The two right triangles are congruent because they share two pairs of equal sides: OB ≅ OD and OE ≅ OF.
$$ OBE \cong ODF $$
From this congruence, we know that corresponding parts of the triangles are equal. In particular, the segments BE ≅ DF are congruent.
$$ \overline{BE} \cong \overline{DF} $$
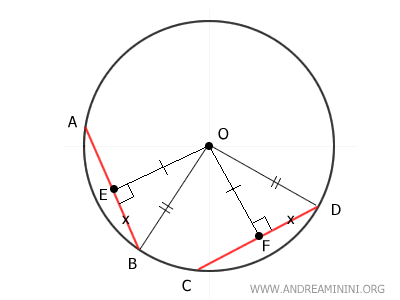
Next, draw segments OA and OC, forming triangles OAB and OCD.
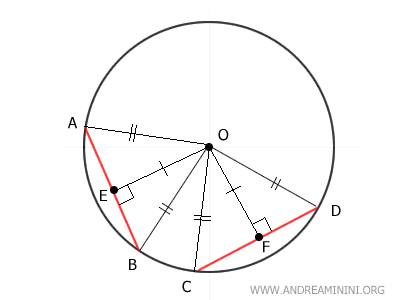
Since OA and OC are radii of the circle, they are congruent to each other OA ≅ OC, and also congruent to the other radii OB and OD:
$$ \overline{OA} \cong \overline{OC} \cong \overline{OB} \cong \overline{OD} $$
Thus, triangles AOB and COD are isosceles triangles, as each has two congruent sides: OA ≅ OB and OC ≅ OD.
In an isosceles triangle, the altitude also serves as the median, so the segments AE ≅ BE and CF ≅ DF are congruent.
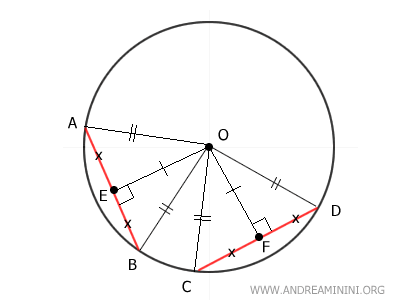
Since we already have BE ≅ DF, doubling these segments leads to the conclusion that 2BE ≅ 2DF.
Because 2BE represents the length of chord AB (i.e., 2BE ≅ AB) and 2DF represents chord CD (i.e., 2DF ≅ CD), it follows that the chords AB and CD are congruent:
$$ \overline{AB} \cong \overline{CD} $$
This proves that two chords equidistant from the center O of a circle are congruent.
B] Two congruent chords are equidistant from the center of the circle
Consider two chords AB and CD, which are congruent by hypothesis, so AB ≅ CD.
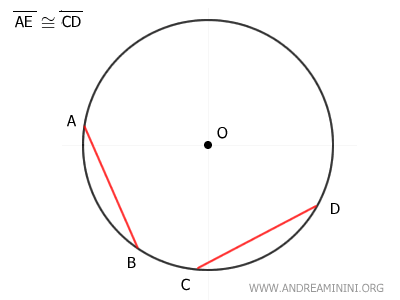
Draw the segments OA, OB, OC, and OD. Since these are all radii, they are congruent: OA ≅ OB ≅ OC ≅ OD.
The triangles OAB and OCD are congruent by the Side-Side-Side (SSS) congruence criterion:
$$ OAB \cong OCD $$
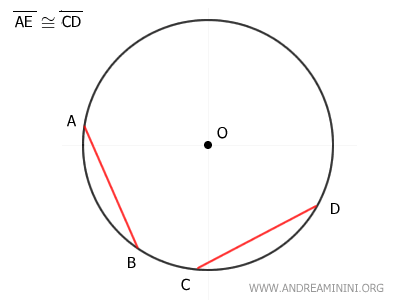
Furthermore, triangles OAB and OCD are both isosceles triangles, since each has two congruent sides: OA ≅ OB and OC ≅ OD.
In an isosceles triangle, the median also functions as the altitude - that is, the segment drawn from the vertex to the midpoint of the opposite side.
In this case, segments OE and OF are the altitudes of the triangles and are congruent: OE ≅ OF, because the triangles themselves are congruent.
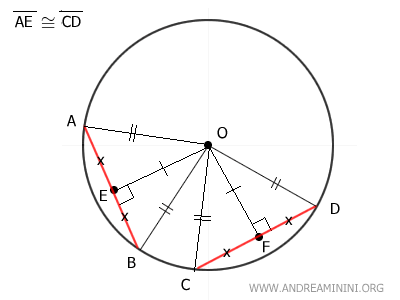
The altitudes OE ≅ OF are perpendicular to the chords and extend from the center O of the circle. Therefore, these segments represent the distance of the chords from the center.
This demonstrates that two congruent chords are equidistant from the center of the circle.
And so on.
