Theorem of the Perpendicular Bisector of a Chord

In a circle, the perpendicular bisector of any chord always passes through the center of the circle.

Proof

Consider a chord AB and let M be its midpoint.

Connect the endpoints A and B of the chord to the center O using the segments OA and OB. This creates triangle ABO.

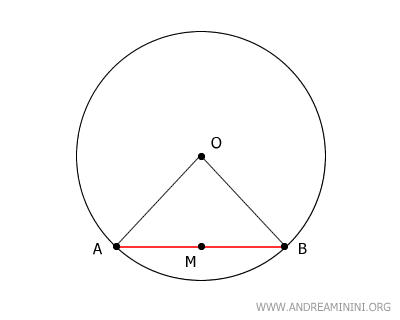
The segments OA and OB are congruent because both are radii of the circle.

$$ \overline{OA} \cong \overline{OB} $$

Since OA and OB are congruent, triangle ABO is an isosceles triangle.

In an isosceles triangle, the median drawn from the vertex O to the midpoint M of the base AB also acts as the altitude, the angle bisector, and the perpendicular bisector.

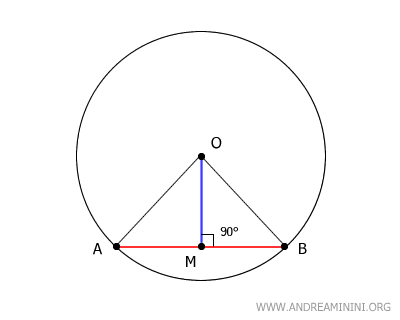
In this case, segment OM serves as the median and simultaneously as the altitude of the triangle. Therefore, OM is perpendicular to AB, forming a right angle of 90°.

Segment OM is also the perpendicular bisector of segment AB because it’s perpendicular and passes through M, the midpoint of AB.

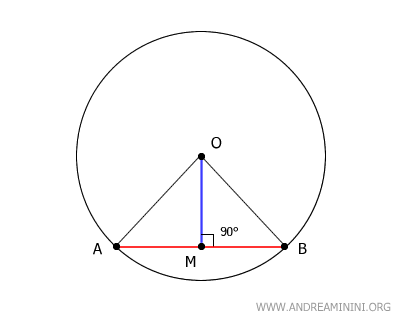
By construction, one endpoint of segment OM coincides with the center O of the circle.

This demonstrates that the perpendicular bisector of a chord always passes through the center of the circle.

And so on.