Theorem of the Diameter Passing Through the Midpoint of a Chord

In a circle, if a diameter passes through the midpoint of a chord that does not pass through the center, then the diameter is perpendicular to that chord.

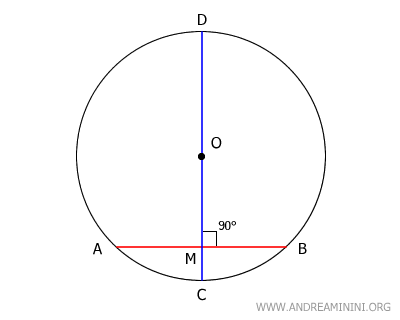
Proof

Consider a chord AB that does not pass through the center O of the circle, and a diameter CD intersecting the midpoint M of the chord.

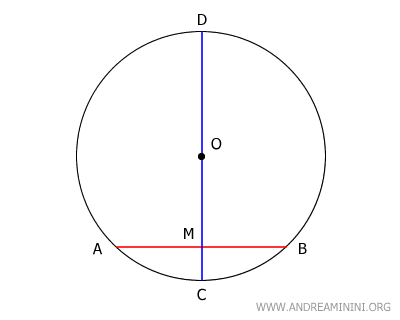
Connect the endpoints A and B of the chord to the center O by drawing segments OA and OB. This forms triangle ABO.

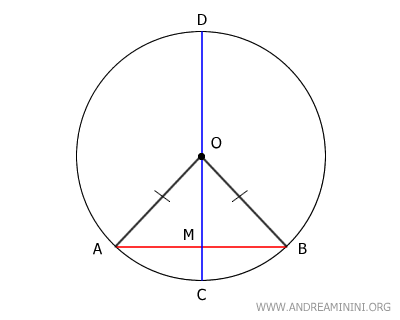
Since OA and OB are both radii of the circle, they are congruent:

$$ \overline{AO} \cong \overline{BO} $$

Having two congruent sides makes triangle ABO an isosceles triangle.

In an isosceles triangle, the median drawn from the vertex to the base not only serves as the median, but also acts as the altitude, angle bisector, and perpendicular bisector.

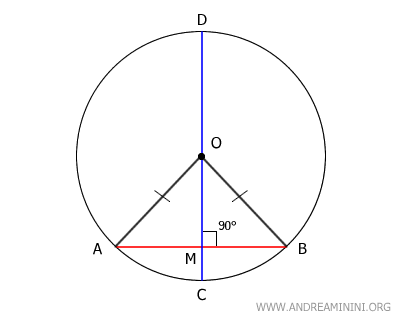
Here, segment OM functions as both the median and the altitude of the triangle. Consequently, OM is perpendicular to AB, forming a right angle of 90°.

Since segment OM lies along diameter CD, we can conclude that the diameter CD is perpendicular to chord AB.

Note. It’s important to point out that this theorem only holds when chord AB does not pass through the center O of the circle. If the chord did pass through O, its midpoint would always coincide with the center of the circle. In that situation, any diameter would pass through the center, forming angles of varying measures. In essence, point O would become the origin of a family of lines radiating outward in all directions.

And so on.