Theorem of Non-Congruent Chords

In a circle, two chords that are not congruent are not equally distant from the center. The shorter chord lies farther from the center and vice versa.

Proof

Let’s consider two non-congruent chords, AB and AC, drawn in a circle, where AC is longer than AB - that is, AC > AB.

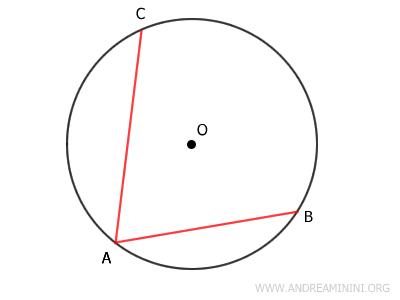
Draw the radii OA, OB, and OC. Naturally, these are all congruent: OA ≅ OB ≅ OC, because a circle is defined as the set of all points equidistant from its center O.

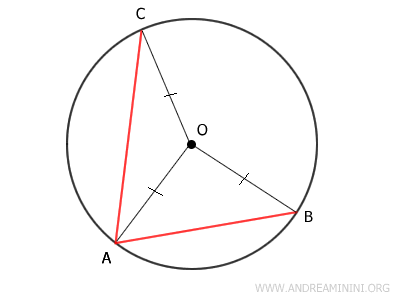
This construction yields two triangles, AOB and AOC.

Both triangles AOB and AOC are isosceles triangles, since each has two congruent sides.

In isosceles triangles, the median also serves as the altitude. Therefore, points M and N are the midpoints of chords AB and AC, respectively.

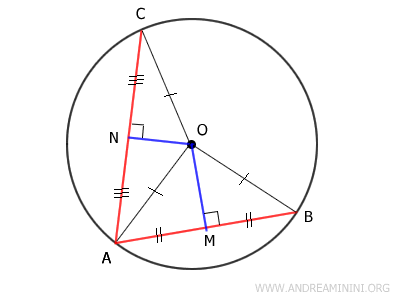
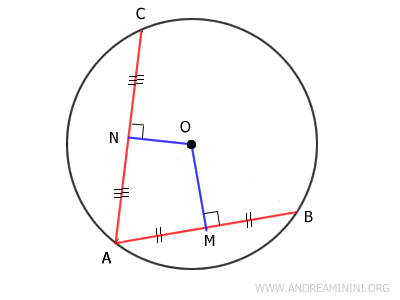
Now draw the segment MN, connecting the midpoints M and N.

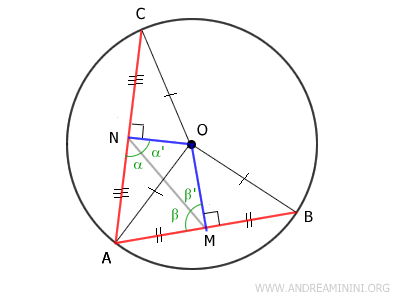
The segment MN forms two pairs of complementary angles:

$$ \alpha + \alpha' = 90^\circ $$

$$ \beta + \beta' = 90^\circ $$

In triangle AMN, side AN is longer than AM because, by our initial hypothesis, chord AC > AB. Since AN is half of AC, and AM is half of AB, it follows that AN > AM:

$$ \overline{AN} > \overline{AM} $$

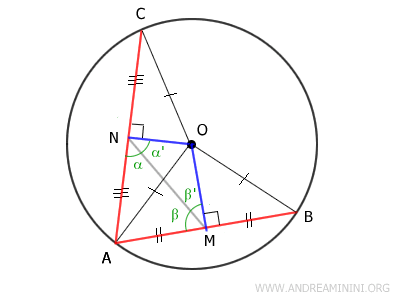
In triangle AMN, if side AN is longer than AM, then their opposite angles follow the same inequality.

Angle β lies opposite side AN, while angle α lies opposite side AM:

$$ \beta > \alpha $$

Since we know that α + α′ = 90° and β + β′ = 90°, the relationship between the complementary angles reverses:

$$ \beta' < \alpha' $$

Given that β' < α', we can apply the same theorem to conclude that the sides opposite these angles obey the same inequality. Thus, ON < OM.

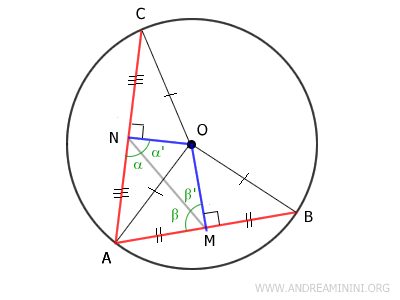
Therefore, segment OM is longer than segment ON:

$$ \overline{OM} > \overline{ON} $$

This demonstrates that the shorter chord AB lies farther from the center (OM > ON) than the longer chord AC.

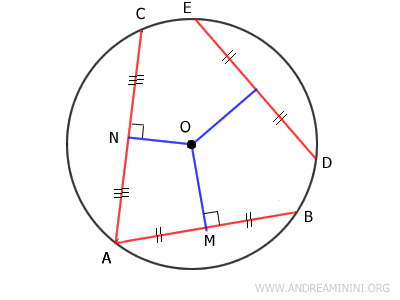
And since any chord DE congruent to AB has the same distance from the center, we can conclude that any chord shorter than AC lies farther from the center.

And so on.