Antisymmetric Relations

What Is an Antisymmetric Relation?

A relation on a set X is called antisymmetric if, for any two distinct elements, whenever a is related to b, then b is not related to a: $$ a R b \ ,\ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$

In other words, no pair of distinct elements in an antisymmetric relation can be mutually related.

For example, the relation “A is greater than or equal to B” is antisymmetric, since if A ≥ B and A ≠ B, then it cannot also be the case that B ≥ A.

This condition allows for bidirectional relationships only when the elements involved are equal.

Distinguishing Antisymmetry from Asymmetry. Although they may appear similar at first glance, antisymmetric and asymmetric relations are fundamentally different. In an antisymmetric relation, mutual relationships are only permitted between identical elements. In an asymmetric relation, no such reciprocity is allowed - regardless of whether the elements are equal or distinct. For instance, the relation “greater than or equal to” is antisymmetric: if A ≥ B and A ≠ B, then B ≥ A cannot also hold. However, the same relation fails to be asymmetric because if A = B, then both A ≥ B and B ≥ A are true, resulting in a symmetric pair.

Antisymmetric relations form a subclass of the relations defined on a set.

A Concrete Example

Let us consider the set:

$$ I = \{ 1, 2, 3, 4 \} $$

Define the relation R as “x is greater than or equal to y”:

$$ R = \{ (4;3), (4;2), (4;1), (3;2), (3;1), (2;1) \} $$

This relation is antisymmetric because, for any two distinct elements x and y, if x ≥ y, then y ≥ x does not hold.

Note. For example, 4 ≥ 3: $$ 4 > 3 $$ But the reverse, 3 ≥ 4, is false: $$ 3 < 4 $$ Hence, the relation meets the criterion for antisymmetry.

When represented as a graph, no two distinct nodes are joined by edges in both directions.

The only bidirectional connections are self-loops, which represent cases where an element is related to itself - e.g., 3 ≥ 3.

Unlike in asymmetric relations, such loops are entirely compatible with antisymmetry.

This is because antisymmetry explicitly concerns relationships between distinct elements only.

Further Observations

Additional insights into antisymmetric relations:

• A relation may be neither symmetric nor antisymmetric. The two properties are not exhaustive nor mutually exclusive.

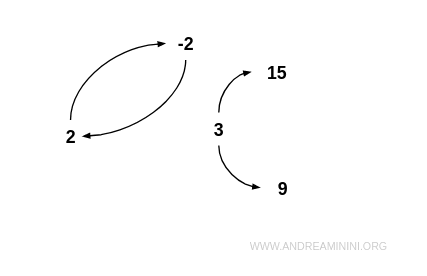
  Example. Consider the set $$ I = \{ -2, 2, 3, 9, 15 \} $$ and the relation R defined as “x is a proper divisor of y”: $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ This relation is not antisymmetric, since - 2 and 2 are mutually related. Yet it is not symmetric either, as 9 is not a proper divisor of 3. Thus, R is neither symmetric nor antisymmetric. In the graph of R, a bidirectional edge connects - 2 and 2, but not all pairs exhibit mutual relations.
  

And so on.