Transitive Relations

What Is a Transitive Relation?

A relation is considered transitive if, for any three elements a, b, and c in a set I, whenever a is related to b and b is related to c, then a must also be related to c. $$ \forall \ a,b,c \in I \ | \ aRb \ , \ bRc \ \Rightarrow aRc $$ This can be illustrated visually as follows:

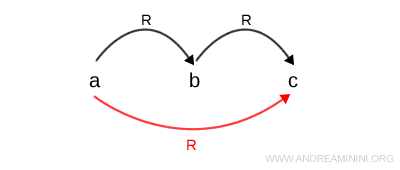
They’re called transitive because they satisfy the transitive property.

For example, if A is the brother of B and B is the brother of C, then A is also the brother of C.

Transitive relations are part of the broader category of relations defined on a set.

Note: Not all relations are transitive. For instance, if A is the mother of B and B is the mother of C, that doesn’t make A the mother of C - so this relation is not transitive.

A Practical Example

Let’s consider the set I:

$$ I = \{ 2 , 4, 6, 8, 10 \} $$

The relation R connects pairs of even numbers.

For instance, 2 and 4 are related because they’re both even:

$$ 2R4 $$

Likewise, 4 and 6 are related for the same reason:

$$ 4R6 $$

By the transitive property, 2 and 6 must also be related - since 2 and 4 form a pair of even numbers, and so do 4 and 6, then 2 and 6 form a valid pair as well:

$$ 2R6 $$

In this case, the transitive property holds for every possible combination of elements in the set I = {2, 4, 6, 8, 10}.

Therefore, the relation R is transitive over the set I.

Note: Transitive relations are often represented using graphs. In a graph, the transitive property is easy to spot through the connections between nodes (the elements of the set). For instance, if there’s an arrow from 2 to 4 and another from 4 to 6, then there must also be a direct arrow from 2 to 6.

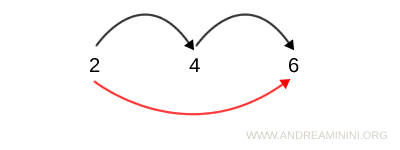
In contrast, two-way tables and Cartesian diagrams don’t readily highlight the transitive property.

Additional Examples

• The relation "x is perpendicular to y" is NOT transitive. If line x forms a 90° angle with line y, and y forms a 90° angle with line z, then x and z form either a 180° angle (a straight line) or a 0° angle (they coincide). In either case, x and z are not perpendicular.

And so on.