Reflexive Relations

What Is a Reflexive Relation?

A relation on a set A is called reflexive if every element of A is related to itself. $$ \forall \ a \in \ A \ , \ aRa $$

In other words, a reflexive relation connects each element in the set to itself.

For instance, the relation "X is the same age as Y" is reflexive because anyone is, naturally, the same age as themselves.

Reflexive relations fall under the broader category of relations defined on a set.

A Concrete Example

Let’s consider the set A:

$$ A = \{ 2,3,4,5,6,7,8,9 \} $$

We define a relation R that links each element of A to its multiples, provided they also belong to the set.

$$ R = \{ (2;2), (2;4), (2;6), (2;8), (3;3), (3;6), (3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4), (4;8), (5;5), (6;6), (7;7), (8;8), (9;9) \} $$

This relation is a subset of the Cartesian product AxA - that is, all possible ordered pairs of elements from A.

We can represent this relation using a double-entry table.

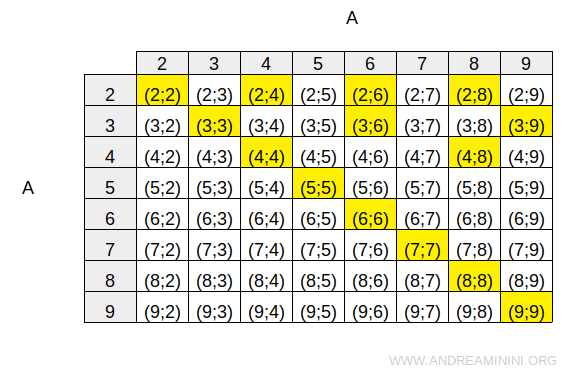
The yellow cells highlight the pairs in AxA that satisfy the relation R.

Notice that every element is related to itself.

The main diagonal of the table contains only ordered pairs that belong to the relation (and are shown in yellow), such as (2;2), (3;3), (4;4), and so on.

This confirms that R is indeed a reflexive relation.

Note. In a graph representation, a relation is reflexive if every node has a loop - that is, an edge connecting it back to itself. This visual clue makes reflexivity immediately apparent.

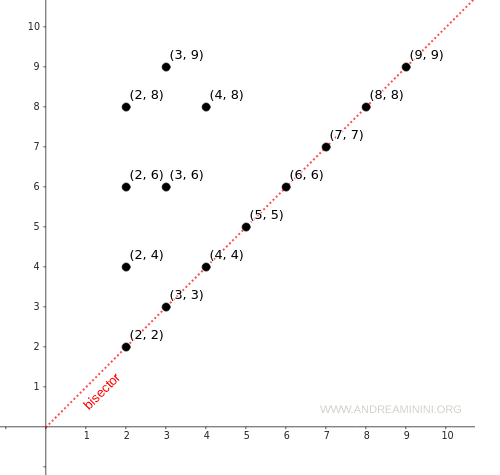
In a Cartesian diagram, a relation is reflexive if all elements of A appear as ordered pairs on the diagonal line (the bisector), according to relation R. Here too, reflexivity can be quickly spotted at a glance.

More Examples

• The relation "x is perpendicular to y" is not reflexive, since no line can form a 90° angle with itself.

And so on.