Symmetric Relations

What Is a Symmetric Relation?

A relation is said to be symmetric if, whenever an element a is related to an element b, then b is also related to a. $$ \forall a,b \in X \ , \ aRb \Rightarrow bRa $$

They’re called "symmetric" because their structure exhibits a visual symmetry when represented graphically.

For example, if X is the brother of Y, then Y is also the brother of X.

Symmetric relations form a subset of the relations defined on a set.

Note. A symmetric relation is classified as an equivalence relation if it is also reflexive and transitive.

A Practical Example

Let’s consider the set:

$$ A = \{ -1, -2, -3, 1, 2, 3 \} $$

Define a relation R that associates each number with its additive inverse.

$$ R = \{ (-1;1), (-2;2), (-3;3), (1;-1), (2;-2), (3;-3) \} $$

This relation is a subset of the Cartesian product AxA.

We can visualize it using a double-entry table.

The table reveals a clear symmetry across the main diagonal.

For every cell that satisfies the relation (highlighted in color), its mirror image across the diagonal also satisfies the relation - both cells are marked identically.

For instance, - 2 is the opposite of 2, and likewise, 2 is the opposite of - 2.

This symmetry becomes even more apparent when the relation is graphed on a Cartesian plane.

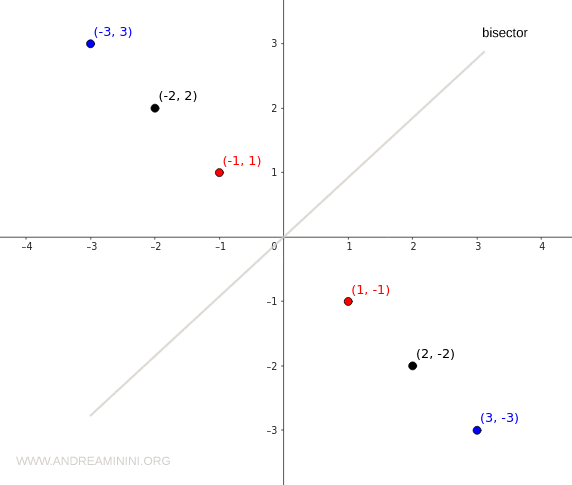
In this case, the symmetry is reflected along the bisector of the diagram.

Note. In a graph-based representation of a symmetric relation, every directed edge from one vertex to another is accompanied by an edge going in the reverse direction.

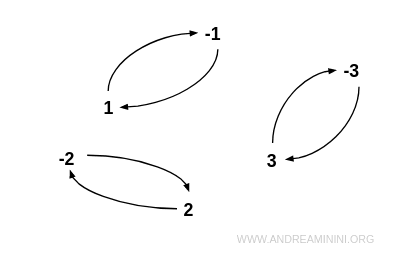
Additional Examples

• The relation "x is perpendicular to y" is symmetric because if line x forms a right angle with line y, then line y also forms a right angle with line x.

Further Remarks

Here are some key points to keep in mind about symmetric relations:

• If a relation is not symmetric, it doesn’t necessarily mean it is asymmetric. There exist relations that are neither symmetric nor asymmetric.
• Symmetry is not the opposite of antisymmetry. It’s possible for a relation to be neither symmetric nor antisymmetric.

And so on.