Inverse Relation

Given a relation aRb defined on the Cartesian product A×B, its inverse relation bR^-1a is a subset of B×A consisting of all pairs (b, a) such that aRb holds true.

In simpler terms, if aRb is a relation from set A to set B, then the inverse relation bR^-1a maps from B back to A.

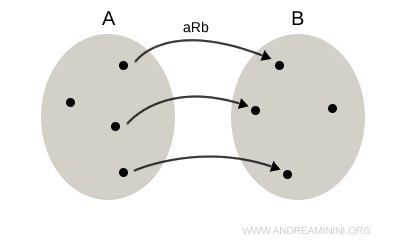
relation example

The inverse relation R^-1 is formed by reversing the order of each pair (a, b) to obtain (b, a).

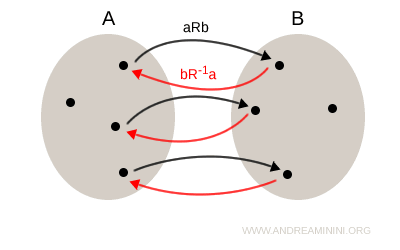
sagittal representation of the inverse relation

Visually, the inverse relation is represented by reversing the direction of the arrows: for every arrow aRb from A to B, there is a corresponding arrow bR^-1a from B back to A.

As a result, the domain of the inverse relation is the codomain of the original:

$$ \text{domain} \ R^{-1} = \text{codomain} \ R $$

And the codomain of the inverse relation is the domain of the original:

$$ \text{codomain} \ R^{-1} = \text{domain} \ R $$

Note: The inverse relation bR^-1a holds if and only if the original relation aRb holds. $$ bR^{-1}a \Leftrightarrow aRb $$

A Practical Example

Let’s consider two finite sets A and B:

$$ A = \{2,3,4,5,6 \} $$

$$ B = \{4,9,16,25,36 \} $$

The relation R maps each element of A to its square in B:

$$ aRb \ : \ b = a^2 $$

This relation is a subset of the Cartesian product A×B, consisting of ordered pairs (a, b):

$$ aRb = \{ (2,4), (3,9), (4,16), (5,25), (6,36) \} \subset A×B $$

Here is the sagittal diagram illustrating the relation aRb:

sagittal diagram of the relation

The inverse relation R^-1 links